Questões de Estatística do ano 2006

Dizemos que Z é estacionário de segunda ordem ou fracamente estacionário se e somente se estiverem satisfeitas as condições, além da (v):

• A. (i) e (ii)
• B. (ii) e (iv)
• C. (i) e (iii)
• D. (i) e (iv)
• E. (ii) e (iii)

De um modo geral, a análise espectral de séries temporais estacionárias decompõe a série em

• A. componentes senoidais com coeficientes aleatórios correlacionados.
• B. uma componente de tendência e uma componente sazonal.
• C. uma componente polinomial, uma componente cíclica e uma componente sazonal.
• D. componentes senoidais com coeficientes aleatórios correlacionados e componentes cossenoidais com coeficientes aleatórios não correlacionados.
• E. componentes senoidais com coeficientes aleatórios não correlacionados.

• A.
• B.
• C.
• D.
• E.

Para o processo ARIMA(1,d,1), onde  o coeficiente autoregressivo e  o coeficiente de médias moveis, é correto afirmar:

• A.

  A função de autocorrelação parcial só é diferente de zero no lag 1.

• B.

  A função de autocorrelação só é diferente de zero nos lags 1 e 2.

• C.

  Se d = 1, o processo é estacionário.

• D.

  A região de admissibilidade é dada por | φ | < 1 e | θ | < 1.

• E.

  A função de autocorrelação é dominada por senóides amortecidas.

Suponha que a série temporal seja afetada por uma intervenção do tipo:

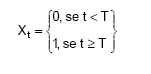
com função de transferência v(B) = 1/(1−B), onde B e o operador translação para o passado, isto é:

Neste caso, a estrutura da função de transferência será representada graficamente por:

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

O modelo ARMA é um modelo

• A.

  não estacionário.

• B.

  estacionário.

• C.

  não estacionário, exclusivamente auto-regressivo.

• D.

  sazonal.

• E.

  estacionário, exclusivamente de média móvel.

Sobre o modelo SARIMA em relação ao modelo ARIMA pode-se afirmar que

• A.

  a eventual sazonalidade do modelo é remota, mantendo-o, na maioria das vezes, nesta forma mais simples de formulação.

• B.

  passa a considerar a variável sazonalidade na estruturação do modelo, tornando-se mais complexo, ao trabalhar com mais variáveis.

• C.

  ao introduzir variáveis do tipo Qui-quadrado, torna o modelo mais complexo, pois trabalha com mais variáveis.

• D.

  ao introduzir variáveis do tipo Log-normal, torna o modelo mais complexo, pois trabalha com mais variáveis.

• E.

  ao introduzir variáveis do tipo Binomial, torna o modelo mais complexo, pois trabalha com mais variáveis.

Assinale a alternativa que representa o desvio padrão amostral da série de dados abaixo (considere na sua resposta a precisão com duas casas decimais).

• A.

  13,50

• B.

  10,80

• C.

  8,76

• D.

  3,29

• E.

  3,67

Calcule a correlação amostral das duas séries abaixo (considere na sua resposta a precisão com duas casas decimais) e assinale a opção que tem a resposta correta.

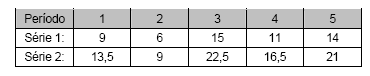
• A.

  –0,32

• B.

  0,32

• C.

  0,73

• D.

  –0,73

• E.

  1