Questões de Estatística do ano 2008

A figura acima apresenta os resultados de um estudo acerca da evolução temporal da temperatura máxima média anual — Y — de 1961 a 2002 e sua relação com o desmatamento em uma área da região amazônica. A tendência de crescimento linear foi obtida pelo método de mínimos quadrados ordinários. De acordo com esse modelo de regressão linear simples, os valores ajustados para a temperatura Y em 1961 e 2002 foram iguais a 22,5 ºC e 24,5 ºC, respectivamente, e o coeficiente de determinação (R²) foi igual a 0,72.

Com base nas informações apresentadas, julgue os itens subseqüentes.

A primeira autocorrelação da série história Y (ou a autocorrelação de Y no lag 1) corresponde ao coeficiente angular da tendência apresentada na figura.

• C. Certo
• E. Errado

Instruções: Para responder às questões de números 59 e 60, considere que uma empresa adotou o modelo Z_i = α + βX_i + γY_i + ε_i para estimar a venda anual de seus produtos com base em observações nos últimos 20 anos.

 Dados:

 I. Zi é o total de vendas, em milhares de reais, no ano i.

 II. X_i é um índice de preços dos produtos da empresa (com relação a uma determinada base), no ano i.

III. Y_i é o gasto com propagandas, em milhares de reais, no ano i.

 IV. ε_i é o erro aleatório com as respectivas hipóteses consideradas para o modelo de regressão linear múltipla.

 V. α, β e γ são parâmetros desconhecidos.

Com a utilização do método dos mínimos quadrados obteve-se a respectiva equação do plano. O quadro de análise de variância correspondente forneceu os seguintes dados: Soma dos quadrados referente à regressão: 0,840 Variação residual: 0,051

O coeficiente de explicação (R²) da regressão é tal que

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

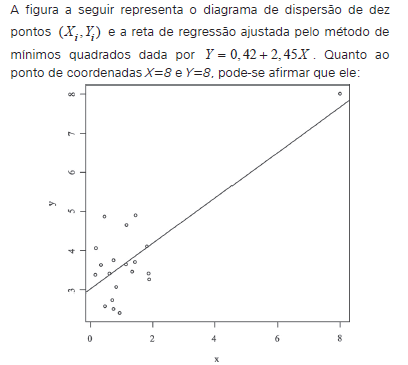
• A.

  é o ponto com maior desvio da reta de regressão.

• B.

  é um ponto influente nessa regressão.

• C.

  é um dado legítimo que indica a relação linear entre X e Y.

• D.

  indica que o modelo é provavelmente heterocedástico.

• E.

  é uma observação incorreta que deve ser eliminada da análise.

Tendo como referência essas informações, julgue os itens de 64 a 76.

O número projetado de leitos por habitante para o ano 2004, com base na extrapolação da tendência linear ajustada, é superior a 5.000.

• E. Errado
• C. Certo

Tendo como referência essas informações, julgue os itens de 64 a 76.

A razão F da tabela ANOVA é a estatística do teste que avalia conjuntamente a significância estatística do coeficiente angular e do intercepto da tendência linear.

• C. Certo
• E. Errado

Tendo como referência essas informações, julgue os itens de 64 a 76.

A razão entre a estimativa do coeficiente pelo seu erro padrão é denominada coeficiente padronizado.

• C. Certo
• E. Errado

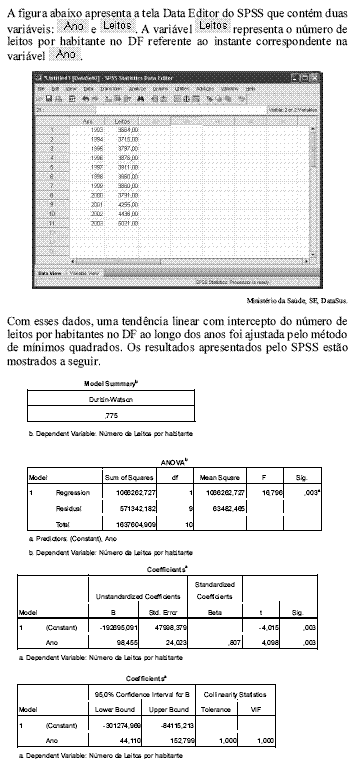
Tendo como referência essas informações, julgue os itens de 64 a 76.

O R ² ajustado (Adjusted R Square) é inferior a 0,7.

• C. Certo
• E. Errado

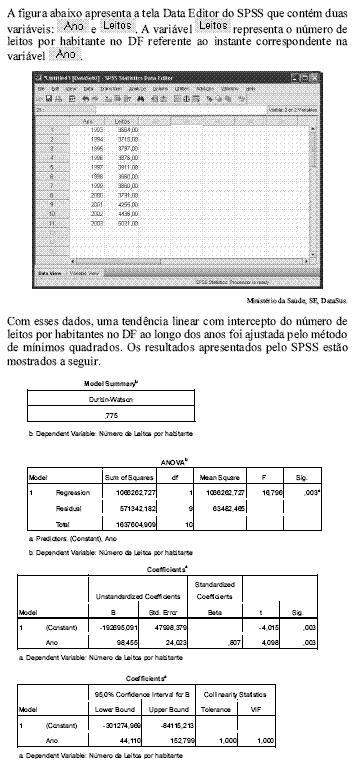
Tendo como referência essas informações, julgue os itens de 64 a 76.

A distribuição amostral da estatística do teste para avaliar a significância do coeficiente angular da reta de regressão é igual à distribuição amostral da estatística do teste para avaliar a significância do intercepto da reta de regressão.

• C. Certo
• E. Errado

Com base nessas informações, julgue os itens de 105 a 108.

Se a distribuição das notas dos alunos for platicúrtica, então a proporção de alunos com menção A será maior que a proporção esperada de alunos com essa menção.

• C. Certo
• E. Errado

Considere as asserções a seguir. Em distribuições assimétricas à direita, a mediana é sempre maior do que a média.

PORQUE

Em distribuições com assimetria positiva, a média é afetada por valores extremos.

Analisando-se as asserções, conclui-se que

• A.

  as duas asserções são verdadeiras, e a segunda é uma justificativa correta da primeira.

• B.

  as duas asserções são verdadeiras, e a segunda não é uma justificativa correta da primeira.

• C.

  a primeira asserção é verdadeira, e a segunda é falsa.

• D.

  a primeira asserção é falsa, e a segunda é verdadeira.

• E.

  a primeira e a segunda asserções são falsas.