Questões de Estatística do ano 2015

Relativamente à análise multivariada, considere:

I. Na análise discriminante, o número de grupos nos quais cada elemento da amostra pertencerá, necessita ser conhecido a priori.

II. Na análise de conglomerados, as variáveis envolvidas não podem ser categóricas ordinais.

III. A análise de correspondência é uma técnica de interdependência que pode ser aplicada a dados não métricos.

IV. A análise de agrupamentos ideal define grupos de objetos com máxima homogeneidade dentro dos grupos, enquanto também tem máxima heterogeneidade entre os grupos.

Está correto o que se afirma APENAS em

• A. I e II.
• B. I e III.
• C. I, III e IV.
• D. III e IV.
• E. II e IV.

Quando se lida com dados secundários ou amostragens efetuadas por terceiros, quatro tipos de erros podem acontecer. São eles:

• A. erros de qualificação, erros de quantificação, erros de delineamento e erros de questionamento.
• B. erros de amostragem, erros de resposta, erros de falta de resposta e erros de delineamento.
• C. erros de configuração, erros de tabulação, erros de amostragem e erros de seleção.
• D. erros de processamento, erros de falta de resposta, erros de entrevista e erros de controle.
• E. erros de formulário, erros de classificação, erros de processamento e erros de verificação.

Para se verificar a natureza e a extensão da associação linear entre duas variáveis, deve-se usar

• A. o teste do qui-quadrado.
• B. a análise de regressão.
• C. o teste “t” de Student.
• D. o coeficiente de correlação de Pearson.
• E. o coeficiente de correlação de Spearman.

Em 3 escolas X, Y e Z é extraída, em cada uma, uma amostra aleatória de 8 redações de seus alunos, com reposição. Após a avaliação de cada uma das 24 redações, que foi realizada independentemente, decide-se, por meio da análise de variância, testar a um determinado nível de significância se as notas médias das populações das notas das 3 escolas são iguais. A tabela abaixo apresenta as notas médias e os respectivos desvios padrões amostrais referentes a cada escola obtidos por meio de estimadores não viesados das variâncias populacionais.

Pelo quadro de análise de variância, tem-se que o valor da estatística F_c (F calculado) utilizado para testar a igualdade das médias das populações das notas das escolas, considerando a distribuição F, é igual a

• A. 8/3.
• B. 16/19.
• C. 2.
• D. 16/3.
• E. 3/2.

Durante n dias, observou-se o número de determinado tipo de ocorrência em uma região. Pela tabela resultante abaixo, foi calculado como sendo 1,75 o valor da média aritmética, em número de ocorrências por dia, ponderada pela quantidade de dias. Também foram calculados os valores das correspondentes mediana (Md) e moda (Mo) desta distribuição.

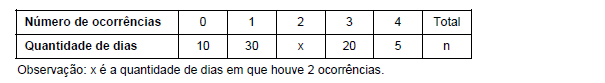
Se x = m(Md + Mo), então m é igual a

• A. 5,0.
• B. 6,0.
• C. 4,0.
• D. 9,0.
• E. 7,5.

A tabela abaixo corresponde às frequências absolutas dos salários de todos os homens e de todas as mulheres que são empregados de uma empresa.

Utilizando o método da interpolação linear para o cálculo da mediana, tem-se que o valor da mediana dos homens é igual a R$ 3.750,00 e o das mulheres é igual a

• A. R$ 3.875,00.
• B. R$ 4.025,00.
• C. R$ 3.925,00.
• D. R$ 3.825,00.
• E. R$ 4.000,00.

Com relação a uma curva de frequência de uma distribuição estatística unimodal, considere as afirmações abaixo:

I. Se a moda for inferior à mediana e a mediana for inferior à média, então esta distribuição é assimétrica à direita.

II. Se a distribuição for assimétrica à esquerda, então isto caracteriza uma curva de frequência leptocúrtica.

III. Se a curva de frequência for platicúrtica, então os dados da distribuição estão fracamente concentrados em torno da moda, caso seja comparado com a curva normal padrão.

IV. Se os dados da distribuição estão fortemente concentrados em torno da moda, então o valor da moda é superior ao valor da mediana e o valor da mediana é superior ao valor da média.

O número de afirmações corretas é

• A. três.
• B. quatro.
• C. duas.
• D. zero.
• E. uma.

Um indicador do desempenho de custo é o índice de Desempenho de Custo (IDC), que é uma medida da eficiência com a qual um projeto vem sendo realizado em termos de custos. O valor do IDC é calculado

• A. multiplicando-se o valor agregado acumulado pelo custo real acumulado.
• B. subtraindo-se o custo real acumulado do valor agregado acumulado.
• C. dividindo-se o custo real acumulado pelo valor agregado acumulado.
• D. subtraindo-se o valor agregado acumulado do custo agregado acumulado.
• E. dividindo-se o valor agregado acumulado pelo custo real acumulado.

Seja uma experiência em que a probabilidade de sucesso é igual a p e as hipóteses H₀: p = k (hipótese nula) e H₁: p = 2k (hi- (pótese alternativa). Determina-se que H₀ será aceita se e somente se o sucesso ocorrer mais que uma vez em uma série de 4 experiências independentes executadas. Se , então a potência deste teste é igual a

• A. 8/27.
• B. 1/9.
• C. 19/27.
• D. 8/9.
• E. 4/9.

Suponha que o número mensal de prisões em flagrante, comunicadas a uma Defensoria Pública de uma determinada região, tenha distribuição de Poisson com média 9. Nessas condições, a probabilidade de serem comunicadas, à Defensoria, pelo menos 4 prisões em flagrante em um período de 10 dias é igual a

• A. 0,575.
• B. 0,425.
• C. 0,525.
• D. 0.475.
• E. 0,555.