Questões de Estatística do ano 2020
Lista completa de Questões de Estatística do ano 2020 para resolução totalmente grátis. Selecione os assuntos no filtro de questões e comece a resolver exercícios.
Estatística - Cálculo de Probabilidades - Centro de Seleção e de Promoção de Eventos UnB (CESPE) - 2020
Um pesquisador deseja estimar a proporção de funcionários públicos que utilizam transporte público como meio de locomoção para ir ao trabalho. Ele pretende obter um erro de, no máximo, 2% com probabilidade de, pelo menos, 95%.
Assinale a opção que indica o número de pessoas que o pesquisador precisará entrevistar para obter o que deseja.
-
A) 9.604
B) 4.802
C) 1.681
D) 2.041
E) 457
Estatística - Conhecimentos de estatística - Centro de Seleção e de Promoção de Eventos UnB (CESPE) - 2020
Ao montar um diagrama de dispersão entre as variáveis idade do réu e as respectivas penas de reclusão cominadas, ambas em anos, um analista judiciário observou fraca correlação negativa.
O coeficiente de correlação de Pearson que melhor descreve essa situação hipotética é
-
A) - 0 ,85.
B) - 0,66.
C) - 0,50.
D) - 0,33.
E) - 0,15.
A distribuição Y apresenta média > mediana > moda. Com essas afirmações, pode-se, corretamente, afirmar que
-
A) a distribuição de X é negativamente assimétrica.
B) a distribuição Y é negativamente assimétrica.
C) a distribuição X é positivamente assimétrica.
D) ambas distribuições X e Y são positivamente assimétricas.
Considere as séries de dados estatísticos, a seguir, e relacione com o tipo de gráfico mais adequado para representá-las.
A sequência que expressa corretamente a correlação entre as colunas é
-
A) (S1,G2): (S2,G3): (S3:G1).
B) (S1,G1): (S2,G3): (S3:G2).
C) (S1,G3): (S2,G2): (S3:G1).
D) (S1,G2): (S2,G1): (S3:G3).
-
A) 7 e 3.
B) 7 e 2.
C) 3 e 7.
D) 7 e 4.
A função densidade de probabilidade (fdp)f de uma variável de aleatória X é dada pela função cujo gráfico é mostrado a seguir.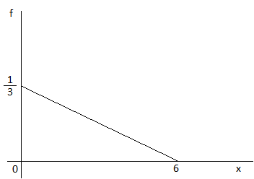
Então, a esperança de X, E(X) é igual a
-
A) 3.
B) 2.
C) 2,1.
D) 1,5.
Considere uma amostra aleatória X1, X2,..., Xn de uma população normal de média µ e variância ?2 = 9 Então, a média e a variância de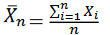 
são, respectivamente,
-
A)
B)
C)
D)
Suponha que a variável aleatória bidimensional (X,Y) tenha função densidade de probabilidade (fdp) conjunta:
Então, o valor de mé igual a
-
A) 1/8.
B) 1/5.
C) 8.
D) 1/3.
O tempo de permanência de uma plateia num show de 3 horas em um teatro é uma variável aleatória com densidade dada por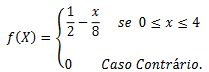
Então, a probabilidade de um expectador, escolhido ao acaso, assistir a mais de 80% do show será aproximadamente de
-
A) 0,12.
B) 0,20.
C) 0,7.
D) 0,16.
-
A) normal com média µ = 2 e variância ?2 = 30.
B) qui-quadrado com µ =5 e variância ?2 = 36.
C) normal com média µ = 5 e variância ?2 = 9.
D) normal com média µ = 5 e variância ?2 = 36.
O Provas e Concursos é um banco de dados de questões de concursos públicos organizadas por matéria, assunto, ano, banca organizadora, etc
