Questões de Estatística do ano 2020

Considere A, B e C três eventos independentes, todos eles com probabilidades positivas e as afirmativas a seguir:

I. A e B^C são independentes.(B^C é o complementar do evento B);
II. A e B ? C são independentes;
III. A ? B e A ? C são independentes.

Está (estão) correta(s) a(s) afirmativa(s)

Suponha que a função densidade de probabilidade (fdp) conjunta da variável (X, Y)seja dada por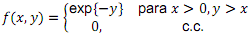



Então, é correto afirmar que

De uma amostra aleatória de tamanho 64 extraída, com reposição, de uma população normalmente distribuída e variância conhecida ?2, obteve-se um intervalo de confiança de 95% igual a [23, 27] para a média ? desta população. Desejando-se obter um intervalo de confiança de 95% para ?, porém com amplitude igual à metade da obtida anteriormente, é necessário extrair da população uma amostra aleatória, com reposição, de tamanho

Em uma empresa de determinado ramo de atividade, utilizando o método de regressão linear, obteve-se a equação de tendência (T) da série temporal abaixo.

Os dados apresentam 10 observações da série temporal Y, que representa o faturamento de uma empresa, em milhões de reais. Supõe-se que essa série é composta apenas de uma tendência T e um ruído branco de média zero e variância constante.

A tendência apresenta a forma T = a + bt, em que a e b foram obtidos usando o método dos mínimos quadrados. Considerando a equação obtida, tem-se que o acréscimo no faturamento do ano t, com t > 1, para o ano (t + 1) é, em milhões de reais, de

Em um relatório de auditoria acerca de uma determinada ocorrência em 8 regiões, obteve-se o gráfico abaixo.
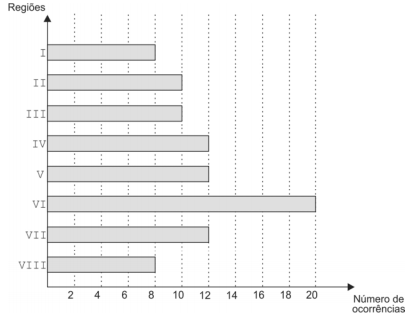Com relação a este relatório, sejam Md a mediana e Me a média aritmética (número de ocorrências por região) correspondentes. O valor da respectiva moda é, então, igual a

O número de empregados de uma empresa é igual a 200, sendo que 60% são homens e o restante mulheres. Nesta empresa, a média aritmética dos salários da população formada pelos salários dos homens é igual a 5 mil reais, com um coeficiente de variação igual a 30%, e a média aritmética dos salários da população formada pelos salários das mulheres também é igual a 5 mil reais, porém com um coeficiente de variação igual a 20%. Considerando a população formada por todos os 200 empregados da empresa, obtém-se que a variância, em mil reais ao quadrado, dos respectivos salários é igual a

A empresa Fernandes Ltda. possui dois investimentos W e Y. O departamento financeiro levantou as seguintes informações: o retorno esperado de W é de 1,5% e o de Y 1,4%. O desvio-padrão é de 10% para W e para Y. Considerando que o nível de risco absoluto é igual para ambas as alternativas de investimento pelo critério da variação relativa (coeficiente de variação), assinale qual investimento é mais arriscado.

O conceito de correlação visa explicar o grau de relacionamento verificado no comportamento de duas ou mais variáveis. Assim, a correlação entre duas variáveis indica a maneira como elas se movem em conjunto. Uma empresa obteve uma covariância entre as variáveis “nível de produção” e “nível da taxa de juros” de ?0,63%; o desvio-padrão da primeira variável foi de 14,08% e da segunda de 4,65%. Ao analisar a correlação entre as variáveis, pode-se afirmar que:

Considerando um levantamento de dados realizado pelo departamento de Recursos Humanos do Município de Capanema/PR, sobre a idade dos servidores públicos, observada a idade que mais se repete no conjunto de dados, tem-se o conceito estatístico de:

Em estatística, considerando a amostra da quantidade de reprografias feitas pelo departamento de Recursos Humanos do Município de Capanema/PR nos meses considerados, calcule a mediana: