Questões de Estatística do ano 2020
Lista completa de Questões de Estatística do ano 2020 para resolução totalmente grátis. Selecione os assuntos no filtro de questões e comece a resolver exercícios.
Considere a variável aleatória X distribuída uniformemente sobre o intervalo [-a; a]. Então, a média e a variância dessa variável são, respectivamente,
-
A) a e a2.
B) (B) 0 e a2/3
C) a/2 e 2a2.
D) 0 e a2/4.
Sejam X e Y duas variáveis quaisquer e definamos X = Y + K. Então, com relação ao Coeficiente de Variação, pode-se afirmar que
-
A) CV(X) < CV(Y), se k<0.
B) CV(X) = CV(Y), se k<0
C) CV(X) < CV(Y), se K>0.
D) CV(X) > CV(Y), se k>0.
Considere as seguintes afirmações:
I. as distribuições de Bernoulli e Binomial apresentam as mesmas características e, portanto, os mesmos parâmetros;
II. repetições independentes de um ensaio de Bernoulli, com a mesma probabilidade de ocorrência de sucesso, dão origem ao modelo Binomial;
III. o Teorema do Limite Central garante que, para n suficientemente grande, a distribuição de Bernoulli pode ser aproximada pela distribuição de Poisson.
Pode-se afirmar que
I. as distribuições de Bernoulli e Binomial apresentam as mesmas características e, portanto, os mesmos parâmetros;
II. repetições independentes de um ensaio de Bernoulli, com a mesma probabilidade de ocorrência de sucesso, dão origem ao modelo Binomial;
III. o Teorema do Limite Central garante que, para n suficientemente grande, a distribuição de Bernoulli pode ser aproximada pela distribuição de Poisson.
Pode-se afirmar que
-
A) somente II está correta.
B) I e II estão corretas.
C) II e III estão corretas.
D) somente III está correta.
Considere o quadro abaixo, representando a distribuição conjunta de X e Y.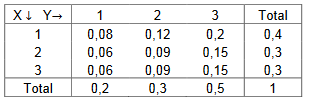
Considere as seguintes afirmações:
I. X e Y são independentes;
II. P(X =1 ou Y=2)=0,14;
III. E(X)=1,9 e E(Y)=2,3.
Pode-se afirmar que
-
A) somente I está correta.
B) I e II estão corretas.
C) I e III estão corretas.
D) Todas as afirmações estão corretas.
Sabe-se que um soro da verdade, quando ministrado a um suspeito, é 90% eficaz quando a pessoa é culpada e 95% eficaz quando a pessoa é inocente. Se o suspeito foi retirado de um grupo em que 90% jamais cometeram qualquer crime, então a probabilidade do soro indicar que o indivíduo é culpado é aproximadamente de
-
A) 0,135.
B) 0,250.
C) 0,950.
D) 0,861.
O gráfico mais adequado para representar uma distribuição de frequência de uma variável nominal é
-
A) Histograma.
B) Diagrama de barras.
C) Polígono de frequências.
D) Polígono de frequências acumuladas.
Para obter o ponto médio de uma classe de intervalos, deve-se
-
A) somar, ao limite superior da classe, metade da sua amplitude de classe.
B) subtrair, do seu limite inferior, metade de sua amplitude de classe e dividir o resultado por 2.
C) somar, ao seu limite inferior, metade de sua amplitude de classe e dividir o resultado por 2.
D) somar, ao limite inferior da classe, metade da sua amplitude de classe.
Uma determinada empresa produz caixas de papelão para embalagens de margarina e afirma que o número de defeitos por caixa se distribui conforme a tabela a seguir:
Node defeito - Node caixas
0 32
1 29
2 10
3 4
4 3
5 1
Considerando-se as informações acima, pode-se afirmar que a
Node defeito - Node caixas
0 32
1 29
2 10
3 4
4 3
5 1
Considerando-se as informações acima, pode-se afirmar que a
-
A) média é 1,3.
B) variável em estudo é qualitativa ordinal.
C) mediana é 1.
D) distribuição é assimétrica à esquerda.
Seja X uniformemente distribuída no intervalo (0,1) e Y = Xn.
A função densidade e a esperança de Y são dadas, respectivamente, por
A função densidade e a esperança de Y são dadas, respectivamente, por
-
A)
B)
C)
D)
A esperança de uma variável aleatória X é igual a 2, ou seja: E(x) = 2. Sabendo-se que a média dos quadrados de X é igual a 9, então os valores da variância e do coeficiente de variação de X são, respectivamente, iguais a
-
A) 5, 5/2
B) 5,?5/2
C) ?5,?5/2
D) ?5/2,5
O Provas e Concursos é um banco de dados de questões de concursos públicos organizadas por matéria, assunto, ano, banca organizadora, etc
