Questões sobre Cálculo de Probabilidades
Lista completa de Questões sobre Cálculo de Probabilidades para resolução totalmente grátis. Selecione os assuntos no filtro de questões e comece a resolver exercícios.
-
A) 0,11.
B) 0,90.
C) 0,68.
D) 0,82.
A variável aleatória X segue a função densidade de probabilidade da forma
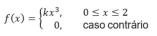
onde k é uma constante real não nula
Com base nesse modelo, assinale com V as afirmativas verdadeiras e com F as falsas.
( ) A probabilidade de a variável aleatória assumir valores menores ou iguais a 1 é 0,50.
( ) O valor de k é 1/4.
( ) O valor esperado da variável aleatória é 1,6.
Assinale a sequência correta.
-
A) F F V
B) V V F
C) F V V
D) V F F
Considere que um estudo foi realizado no ambulatório de um hospital com vários testes de triagem para detecção de certa doença. A sensibilidade e a especificidade do teste são 0,80 e 0,90, respectivamente.
Sabendo-se que a probabilidade de uma pessoa ter a doença é 0,40 na população de interesse, analise as afirmativas a seguir.
I. A probabilidade de ocorrer um falso positivo no próximo teste é 0,10.
II. A probabilidade de o próximo teste apresentar resultado negativo é 0,60.
III. A probabilidade de uma pessoa ter a doença, se seu teste apresentou resultado positivo, é 16/19.
IV. A probabilidade de uma pessoa não ter a doença, se seu teste apresentou resultado negativo, é 27/31.
Está(ão) correta(s) a(s) afirmativa(s)
-
A) II, apenas.
B) II e IV, apenas.
C) I e III, apenas.
D) I, III e IV, apenas.
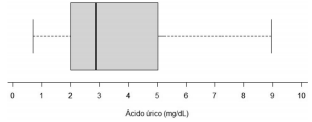
Supondo que três adultos dessa população sejam selecionados aleatoriamente, a probabilidade de pelo menos um deles ter nível de ácido úrico acima de 5 mg/dL é:
-
A) 0,25.
B) 0,75.
C) 0,58.
D) 0,42.
Estatística - Cálculo de Probabilidades - Centro de Seleção e de Promoção de Eventos UnB (CESPE) - 2021
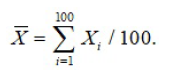
Estatística - Cálculo de Probabilidades - Centro de Seleção e de Promoção de Eventos UnB (CESPE) - 2020
A partir de uma amostra aleatória simples de tamanho n, sabe-se que a média aritmética de uma variável X foi igual a 3. Considerando que os valores possíveis para a variável X sejam -1 e +4, julgue o item que se segue.
A distribuição da variável X é simétrica em torno da sua média amostral.
Estatística - Cálculo de Probabilidades - Centro de Seleção e de Promoção de Eventos UnB (CESPE) - 2020
-
A) 0,2.
B) 0,3.
C) 0,4.
D) 0,5.
E) 0,6.
Estatística - Cálculo de Probabilidades - Centro de Seleção e de Promoção de Eventos UnB (CESPE) - 2020
Se ? representar um espaço amostral de determinado experimento aleatório, A d ? e B d ? forem dois eventos com P(A) = 0,4 e P(B) = 0,8 e se 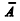 e
e 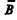 forem, respectivamente, os eventos complementares de A e B, então
forem, respectivamente, os eventos complementares de A e B, então
-
A)

B)

C)

D)

E)

Estatística - Cálculo de Probabilidades - Centro de Seleção e de Promoção de Eventos UnB (CESPE) - 2020
A função de densidade de probabilidade de uma variável aleatória contínua X é expressa por:
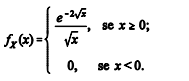
Se 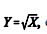 então a função de densidade da variável Y para y
então a função de densidade da variável Y para y 0 é expressa por
0 é expressa por
-
A)

B)

C)

D)

E)

Estatística - Cálculo de Probabilidades - Centro de Seleção e de Promoção de Eventos UnB (CESPE) - 2020
Um pesquisador deseja estimar a proporção de funcionários públicos que utilizam transporte público como meio de locomoção para ir ao trabalho. Ele pretende obter um erro de, no máximo, 2% com probabilidade de, pelo menos, 95%.
Assinale a opção que indica o número de pessoas que o pesquisador precisará entrevistar para obter o que deseja.
-
A) 9.604
B) 4.802
C) 1.681
D) 2.041
E) 457


