Questões sobre Média

Considere que U ₁ , U ₂ e U ₃ sejam cópias independentes de uma distribuição uniforme, com média igual a 6 e variância igual a 3. Com base nessas informações, julgue os próximos itens acerca da soma S = U ₁ % U ₂ % U ₃ .

A média correspondente à variável transformada 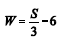é igual a zero, e a variância igual a 1.

• C. Certo
• E. Errado

Um porto possui dois cais para embarque ou desembarque de passageiros. Cada cais atende a uma única embarcação por vez, e assim que a operação de embarque ou desembarque é concluída, a embarcação deixa imediatamente o local para que a próxima embarcação possa ser atracada ao cais. O número de embarcações que chegam a esse porto por dia, X, segue um processo de Poisson com taxa de chegada igual a 1 embarcação/dia. Se uma embarcação chega ao porto no instante em que os dois cais estão ocupados, ela entra em uma fila única; não havendo limites para o tamanho da fila. Em cada cais, a taxa de serviço é igual a 1,5 embarcação/dia.

Considerando as informações apresentadas acima e que se trata, nessa situação, de um modelo de fila M/M/2 baseado no processo de vida e morte com taxas de chegada e de serviço constantes, julgue os itens subsequentes.

Em média, o tempo gasto na operação de embarque ou desembarque, é superior a 1 dia/embarcação.

• C. Certo
• E. Errado

Um porto possui dois cais para embarque ou desembarque de passageiros. Cada cais atende a uma única embarcação por vez, e assim que a operação de embarque ou desembarque é concluída, a embarcação deixa imediatamente o local para que a próxima embarcação possa ser atracada ao cais. O número de embarcações que chegam a esse porto por dia, X, segue um processo de Poisson com taxa de chegada igual a 1 embarcação/dia. Se uma embarcação chega ao porto no instante em que os dois cais estão ocupados, ela entra em uma fila única; não havendo limites para o tamanho da fila. Em cada cais, a taxa de serviço é igual a 1,5 embarcação/dia.

Considerando as informações apresentadas acima e que se trata, nessa situação, de um modelo de fila M/M/2 baseado no processo de vida e morte com taxas de chegada e de serviço constantes, julgue os itens subsequentes.

Em média, o tempo entre a chegada de uma embarcação e a da embarcação seguinte é superior a 0,9 dia.

• C. Certo
• E. Errado

Um porto possui dois cais para embarque ou desembarque de passageiros. Cada cais atende a uma única embarcação por vez, e assim que a operação de embarque ou desembarque é concluída, a embarcação deixa imediatamente o local para que a próxima embarcação possa ser atracada ao cais. O número de embarcações que chegam a esse porto por dia, X, segue um processo de Poisson com taxa de chegada igual a 1 embarcação/dia. Se uma embarcação chega ao porto no instante em que os dois cais estão ocupados, ela entra em uma fila única; não havendo limites para o tamanho da fila. Em cada cais, a taxa de serviço é igual a 1,5 embarcação/dia.

Considerando as informações apresentadas acima e que se trata, nessa situação, de um modelo de fila M/M/2 baseado no processo de vida e morte com taxas de chegada e de serviço constantes, julgue os itens subsequentes.

Em média, o número total de embarcações presentes no porto, atracados no cais ou na fila, é maior ou igual a 1 embarcação/dia.

• C. Certo
• E. Errado

Um porto possui dois cais para embarque ou desembarque de passageiros. Cada cais atende a uma única embarcação por vez, e assim que a operação de embarque ou desembarque é concluída, a embarcação deixa imediatamente o local para que a próxima embarcação possa ser atracada ao cais. O número de embarcações que chegam a esse porto por dia, X, segue um processo de Poisson com taxa de chegada igual a 1 embarcação/dia. Se uma embarcação chega ao porto no instante em que os dois cais estão ocupados, ela entra em uma fila única; não havendo limites para o tamanho da fila. Em cada cais, a taxa de serviço é igual a 1,5 embarcação/dia.

Considerando as informações apresentadas acima e que se trata, nessa situação, de um modelo de fila M/M/2 baseado no processo de vida e morte com taxas de chegada e de serviço constantes, julgue os itens subsequentes.

Sabendo-se que 1 dia corresponde a 24 horas, o tempo médio de espera na fila é inferior a 1 hora/embarcação.

• C. Certo
• E. Errado

Um porto possui dois cais para embarque ou desembarque de passageiros. Cada cais atende a uma única embarcação por vez, e assim que a operação de embarque ou desembarque é concluída, a embarcação deixa imediatamente o local para que a próxima embarcação possa ser atracada ao cais. O número de embarcações que chegam a esse porto por dia, X, segue um processo de Poisson com taxa de chegada igual a 1 embarcação/dia. Se uma embarcação chega ao porto no instante em que os dois cais estão ocupados, ela entra em uma fila única; não havendo limites para o tamanho da fila. Em cada cais, a taxa de serviço é igual a 1,5 embarcação/dia.

Considerando as informações apresentadas acima e que se trata, nessa situação, de um modelo de fila M/M/2 baseado no processo de vida e morte com taxas de chegada e de serviço constantes, julgue os itens subsequentes.

Em 18 dias de funcionamento do porto, espera-se que, em média, em apenas um desses dias haja fila de embarcações.

• C. Certo
• E. Errado

Se a = 0,5 e b = 1,5, então a média de X é superior a 0,50.

• C. Certo
• E. Errado

A média amostral dos valores X₁, X₂, ..., X_n é o estimador de mínimos quadrados para a média da distribuição das perdas X.

• C. Certo
• E. Errado

A média 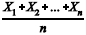 é um estimador não-tendencioso para a média da distribuição das perdas X.

• C. Certo
• E. Errado

O número esperado de pessoas aguardando atendimento na fila é superior a 1 pessoa/minuto.

• C. Certo
• E. Errado