Questões sobre Média
Lista completa de Questões sobre Média para resolução totalmente grátis. Selecione os assuntos no filtro de questões e comece a resolver exercícios.
Considerando um vetor aleatório (X, Y) distribuído na função de densidade conjunta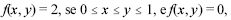 
caso contrário, julgue os itens a seguir.
A média de Y é inferior a 0,5.
- C. Certo
- E. Errado
Considere que X1, X2, ..., Xn seja uma amostra aleatória simples de uma distribuição X, cuja função de densidade é dada por para 
para x < 0 ou x > 
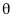em que 
> 0. Com base nessas informações, julgue os itens a seguir.
A média amostral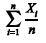 
é o estimador de máxima verossimilhança para .
- C. Certo
- E. Errado
Assinale a opção correta.
A esperança completa de vida de uma pessoa ao nascer é igual a:
- A.
um (1,0)
- B.
Zero (0,0)
- C.
0,5 (meio)
- D.
- E.
Uma distribuição de freqüência com dados agrupados em classe forneceu os pontos médios de classes m e as respectivas freqüências absolutas f abaixo:
m f
49 7
52 15
55 12
58 5
61 1
Calcule a média aritmética simples dos dados.
- A.
52.
- B.
52,25.
- C.
53,35.
- D.
54,15.
- E.
55.
Apesar de uma característica numérica supostamente possuir distribuições com variâncias diferentes em duas populações distintas, deseja-se testar a hipótese estatística da igualdade das duas médias. Assim, da primeira população retira-se uma amostra aleatória simples de tamanho 9 e da segunda população retira-se outra amostra aleatória simples independente de tamanho 16. A característica medida na amostra da primeira população tem média 83 e desvio-padrão amostral 7, enquanto a característica medida na amostra da segunda população tem média 81 e desvio-padrão amostral 8. Obtenha o valor mais próximo do erro padrão da diferença estimada entre as médias.
- A.
1,05.
- B.
1,92.
- C.
2,26.
- D.
2,82.
- E.
3,07.
Seja T um estimador de um parâmetro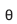 
de uma população. Se E(T) = 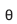, diz-se que T é um estimador de :
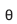- A.
Eficiente.
- B.
Não enviesado.
- C.
Consistente.
- D.
De mínimos quadrados.
- E.
De máxima verossimilhança.
O raio de drenagem, R, é o raio de um círculo de área A de drenagem de um poço. Em um estudo estatístico, a média aritmética e o desvio-padrão amostral dos raios de drenagem de uma amostra aleatória de 10 poços foram, respectivamente, iguais a 200 metros e 50 metros. Com relação a essa situação, considerando-se que a área de drenagem de um poço seja dada por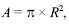 
, então a média aritmética das áreas de drenagem dos poços observados no estudo em questão será igual a
- A.
- B.
- C.
- D.
- E.
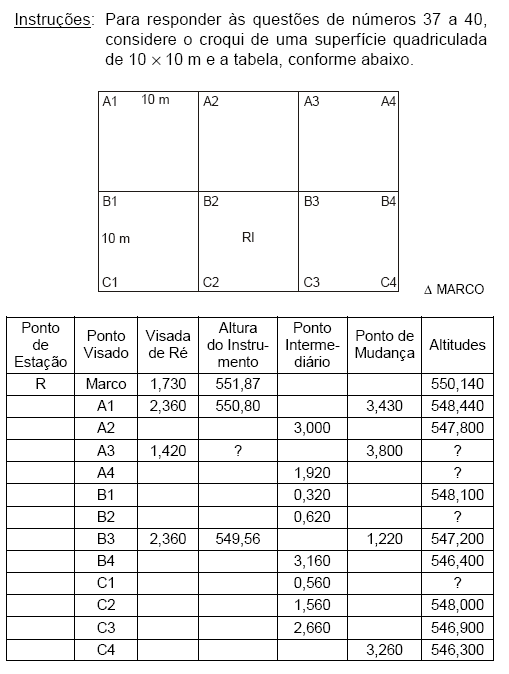
A cota média do terreno é igual a
- A.
547,833.
- B.
547,162.
- C.
548,432.
- D.
547,926.
- E.
547,453.
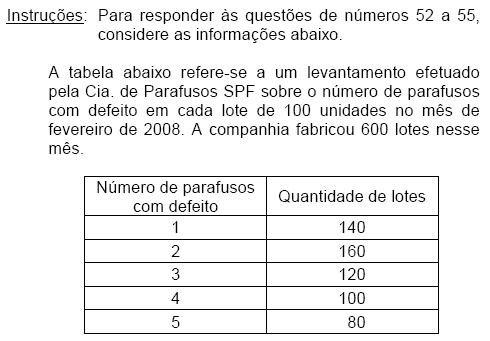
A média aritmética do número de parafusos com defeito dessa população corresponde a
- A.
2,1
- B.
2,2
- C.
2,4
- D.
2,5
- E.
2,7
Uma amostra aleatória simples de tamanho 10 de uma densidade uniforme no intervalo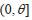 
forneceu os seguintes dados:
2,12 3,46 5,90 7,34 5,31 7,88 6,02 6,54 1,07 0,38
A estimativa de máxima verossimilhança da média dessa densidade é:
- A.
3,94.
- B.
4,32.
- C.
4,48.
- D.
4,62.
- E.
6,02.
O Provas e Concursos é um banco de dados de questões de concursos públicos organizadas por matéria, assunto, ano, banca organizadora, etc
