Questões sobre Probabilidade

O número diário - X - de pacientes que chegam a um pequeno hospital municipal segue um processo de Poisson homogêneo. Sabe-se que a probabilidade de chegar pelo menos 1 paciente em um determinado dia, P(X $ 1), é igual a 1 ! e!8, em que e é o número de Euler (ou base dos logaritmos neperianos). Considere que 1 dia equivale a um período de 24 horas. Com base nessas informações, julgue os itens a seguir.

1nP(X = 0) = 8.

• C. Certo
• E. Errado

O número diário - X - de pacientes que chegam a um pequeno hospital municipal segue um processo de Poisson homogêneo. Sabe-se que a probabilidade de chegar pelo menos 1 paciente em um determinado dia, P(X $ 1), é igual a 1 ! e!8, em que e é o número de Euler (ou base dos logaritmos neperianos). Considere que 1 dia equivale a um período de 24 horas. Com base nessas informações, julgue os itens a seguir.

P(X = 7) < P(X = 8).

• C. Certo
• E. Errado

O número diário - X - de pacientes que chegam a um pequeno hospital municipal segue um processo de Poisson homogêneo. Sabe-se que a probabilidade de chegar pelo menos 1 paciente em um determinado dia, P(X $ 1), é igual a 1 ! e!8, em que e é o número de Euler (ou base dos logaritmos neperianos). Considere que 1 dia equivale a um período de 24 horas. Com base nessas informações, julgue os itens a seguir.

A probabilidade de chegar exatamente 1 paciente entre 9 h e 12 h de determinado dia é igual a        .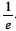

• C. Certo
• E. Errado

O número diário - X - de pacientes que chegam a um pequeno hospital municipal segue um processo de Poisson homogêneo. Sabe-se que a probabilidade de chegar pelo menos 1 paciente em um determinado dia, P(X $ 1), é igual a 1 ! e!8, em que e é o número de Euler (ou base dos logaritmos neperianos). Considere que 1 dia equivale a um período de 24 horas. Com base nessas informações, julgue os itens a seguir.

Considere que, em certo dia, um paciente chega ao hospital às 16 h. A probabilidade do próximo paciente chegar ao hospital até as 19 h do mesmo dia é igual a     .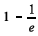

• C. Certo
• E. Errado

Para que um município possa participar de um projeto na área educacional, a média das notas dos estudantes de 5.ª série a 8.ª série das escolas públicas localizadas nesse município deverá ser igual ou superior a 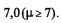  Como não foi possível coletar os dados de todos os estudantes, retirou-se uma amostra aleatória simples de 625 estudantes. Por um teste estatístico, não há evidências estatísticas contra a hipótese de que as notas dos estudantes seguem uma distribuição normal. A nota média observada na amostra foi igual a 6,5 e o desvio padrão amostral foi igual a 2,5. Considerando a situação hipotética apresentada no texto, julgue os itens que se seguem.

A probabilidade de significância (ou nível descritivo) do teste 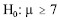versus 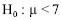é superior a 0,025.

• C. Certo
• E. Errado

Para que um município possa participar de um projeto na área educacional, a média das notas dos estudantes de 5.ª série a 8.ª série das escolas públicas localizadas nesse município deverá ser igual ou superior a 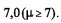  Como não foi possível coletar os dados de todos os estudantes, retirou-se uma amostra aleatória simples de 625 estudantes. Por um teste estatístico, não há evidências estatísticas contra a hipótese de que as notas dos estudantes seguem uma distribuição normal. A nota média observada na amostra foi igual a 6,5 e o desvio padrão amostral foi igual a 2,5. Considerando a situação hipotética apresentada no texto, julgue os itens que se seguem.

Uma verificação descritiva da normalidade desse conjunto de dados pode ser feita por meio de um gráfico de probabilidade normal.

• C. Certo
• E. Errado

Estudo realizado entre jovens recém-formados mostrou que a probabilidade de um jovem investir no mercado financeiro é igual a 0,60. Esse mesmo estudo apontou que a probabilidade de um jovem investir no mercado financeiro e, ao mesmo tempo, estar disposto a assumir riscos sérios é igual a 0,48. Entre os jovens que não investem no mercado financeiro, todos foram considerados como aqueles que não estão dispostos a assumir riscos sérios. E, finalmente, o estudo mostrou que a disposição em assumir riscos sérios independe do gênero (masculino ou feminino).

Com base nessas informações, julgue os itens subseqüentes.

Sabe-se que determinado jovem não está disposto a assumir riscos sérios. Nessa situação, a probabilidade de esse jovem investir no mercado financeiro é superior a 0,21.

• C. Certo
• E. Errado

Uma moeda viciada, ao ser lançada, cai com a cara para cima (cara) em 60% dos casos e com a coroa para cima (coroa) em 40% dos casos. Com base nessas informações, julgue os itens a seguir.

Após lançar a moeda duzentas vezes, espera-se que a quantidade de ocorrências de cara seja o dobro da de coroa .

• C. Certo
• E. Errado

Considere-se que a secretaria de saúde de uma prefeitura municipal tenha realizado um estudo sobre a utilização de medicamentos sem prescrição médica e que esse estudo tenha mostrado que a probabilidade de uma pessoa (homem ou mulher) se automedicar é igual a 0,8 e, ainda, que a probabilidade de uma mulher se automedicar é 4 vezes maior que a de um homem.

 

Com base nessa situação hipotética e nas informações apresentadas, julgue os itens que se seguem.

A probabilidade de uma pessoa não se automedicar é inferior a 0,25.

• C. Certo
• E. Errado

Considere-se que a secretaria de saúde de uma prefeitura municipal tenha realizado um estudo sobre a utilização de medicamentos sem prescrição médica e que esse estudo tenha mostrado que a probabilidade de uma pessoa (homem ou mulher) se automedicar é igual a 0,8 e, ainda, que a probabilidade de uma mulher se automedicar é 4 vezes maior que a de um homem.

 

Com base nessa situação hipotética e nas informações apresentadas, julgue os itens que se seguem.

Do conjunto de pessoas que se automedicam, 20% são do sexo masculino.

• C. Certo
• E. Errado