Questões sobre Regressão

• A. 60
• B. 80
• C. 120
• D. 160
• E. 200

O número de unidades vendidas de um produto por uma empresa apresentou, por meio de um estudo realizado, uma tendência linear de crescimento ao longo do tempo com sazonalidade. A equação da reta de tendência obtida foi Yt = 10 + 50t, em que Yt é o número de unidades vendidas em t, que representa o trimestre correspondente das vendas (t = 1 corresponde ao primeiro trimestre de 2001, t = 2 corresponde ao segundo trimestre de 2001, e assim sucessivamente). Verificando que os movimentos apresentados estavam associados ao nível de tendência, a empresa optou por utilizar o modelo multiplicativo para apurar sua previsão de vendas, usando os fatores sazonais abaixo:

A previsão de vendas, em unidades, para o segundo trimestre de 2007 é

• A. 1.332
• B. 1.392
• C. 1.452
• D. 1.512
• E. 1.572

A quantidade de sólidos totais (Y) na água está relacionada com a sua condutividade elétrica (X), segundo um modelo de regressão linear simples na forma Y = aX + b + E, em que a e b são os coeficientes do modelo e E representa uma variável aleatória normal com média zero e desvio padrão igual a F. Por máxima verossimilhança, o modelo ajustado foi 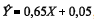, e as estimativas dos desvios padrões de Y e de X foram, respectivamente, iguais a 800 e 1.000. A condutividade média da água foi igual a 2.000. Com base nessas informações, julgue os itens seguintes.

De acordo com o critério dos mínimos quadrados, as estimativas dos coeficientes a e b são, respectivamente, iguais a 0,60 e 0,03.

• C. Certo
• E. Errado

A quantidade de sólidos totais (Y) na água está relacionada com a sua condutividade elétrica (X), segundo um modelo de regressão linear simples na forma Y = aX + b + E, em que a e b são os coeficientes do modelo e E representa uma variável aleatória normal com média zero e desvio padrão igual a F. Por máxima verossimilhança, o modelo ajustado foi 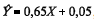, e as estimativas dos desvios padrões de Y e de X foram, respectivamente, iguais a 800 e 1.000. A condutividade média da água foi igual a 2.000. Com base nessas informações, julgue os itens seguintes.

A co-variância entre a quantidade de sólidos totais e a condutividade elétrica da água é superior a 100.

• C. Certo
• E. Errado

A partir das informações apresentadas no texto, assinale a opção incorreta.

• A.

  Mais de 90% da variação total é explicada pelo modelo.

• B.

  A estimativa de é igual ao quadrado médio do erro.

• C.

  A variância amostral de Y é superior a 300

• D.

  A razão F dos dados apresentados na tabela de análise de variância é menor ou igual a 1.

Os métodos quantitativos, incluindo-se aí o cômputo de índices relevantes, são cruciais para o desenvolvimento da economia. A respeito desse tema, julgue os itens seguintes.

No modelo de regressão linear simples, o coeficiente de determinação (R²) é igual ao coeficiente amostral de correlação entre a variável dependente (y) e a variável independente (x).

• C. Certo
• E. Errado

Uma balança foi avaliada quanto ao grau de concordância entre o resultado da medição (Y) e o valor verdadeiro da grandeza medida (X). A partir dessa avaliação foi possível estabelecer uma relação linear na forma Y = aX + b + Z, em que a e b são os coeficientes do modelo e Z representa o erro aleatório que possui média zero e variância igual a <. A tabela abaixo apresenta algumas estatísticas descritivas a respeito de Y, X e Z.

A estimativa de mínimos quadrados para o coeficiente b é igual a 0,5 - Z.

• C. Certo
• E. Errado

Uma balança foi avaliada quanto ao grau de concordância entre o resultado da medição (Y) e o valor verdadeiro da grandeza medida (X). A partir dessa avaliação foi possível estabelecer uma relação linear na forma Y = aX + b + Z, em que a e b são os coeficientes do modelo e Z representa o erro aleatório que possui média zero e variância igual a <. A tabela abaixo apresenta algumas estatísticas descritivas a respeito de Y, X e Z.

A estimativa de mínimos quadrados  é igual a 1.

• C. Certo
• E. Errado

Uma balança foi avaliada quanto ao grau de concordância entre o resultado da medição (Y) e o valor verdadeiro da grandeza medida (X). A partir dessa avaliação foi possível estabelecer uma relação linear na forma Y = aX + b + Z, em que a e b são os coeficientes do modelo e Z representa o erro aleatório que possui média zero e variância igual a <. A tabela abaixo apresenta algumas estatísticas descritivas a respeito de Y, X e Z.

A estatística denominada média dos quadrados dos erros (error mean square) é um estimador não tendencioso para V.

• C. Certo
• E. Errado

Uma balança foi avaliada quanto ao grau de concordância entre o resultado da medição (Y) e o valor verdadeiro da grandeza medida (X). A partir dessa avaliação foi possível estabelecer uma relação linear na forma Y = aX + b + Z, em que a e b são os coeficientes do modelo e Z representa o erro aleatório que possui média zero e variância igual a <. A tabela abaixo apresenta algumas estatísticas descritivas a respeito de Y, X e Z.

O coeficiente de variação de Y é inferior ao coeficiente de variação de X.

• C. Certo
• E. Errado