Questões sobre Regressão

Com o objetivo de diminuir os casos de afogamento na temporada de 2015, uma prefeitura de uma cidade litorânea encomendou estudos estatísticos que identificassem prováveis fatores de risco.

Aplicando o modelo estatístico de regressão linear aos dados da tabela abaixo, podemos afirmar que:

• A. Os dados são linearmente correlacionados e podemos concluir que o consumo excessivo de sorvete aumenta o risco de afogamento.
• B. Há uma correlação não linear entre os dados e a correlação entre eles é provavelmente espúria.
• C. Há uma correlação não linear entre os dados e podemos concluir que o consumo excessivo de sorvete aumenta o risco de afogamento.
• D. Os dados são linearmente correlacionados e a correlação entre eles é provavelmente espúria.
• E. Não há correlação estatística entre os dados.

Considere os resultados a seguir.

Sobre os coeficientes do modelo de regressão linear múltipla, é correto afirmar que

• A. β1 é significativo ao nível de 1% de significância.
• B. β2 é significativo ao nível de 10% de significância.
• C. β0 e β2 são significativos ao nível de 5% de significância.
• D. β1 e β2 não são significativos ao nível de 5% de significância.

• A. 0,7 salários mínimos.
• B. 0,6 salários mínimos.
• C. 0,5 salários mínimos.
• D. 0,4 salários mínimos.
• E. 0,3 salários mínimos.

Considerando os resultados apresentados, é INCORRETO afirmar que o(a)

• A. amostra utilizada tem tamanho igual a 21.
• B. valor b1 (estimativa para ¦Â1) ¨¦ maior que zero.
• C. valor f (estat¨ªstica do teste F da ANOVA) ¨¦ 128,8.
• D. coeficiente de determinação ¨¦, aproximadamente, 0,88.
• E. teste t (t₀ = 11,35, valor ¡§Cp = 0,000) indica que existe correlação significativa entre X e Y.

Sobre o coeficiente de determinação na regressão linear simples é correto afirmar que

• A. mede a capacidade de predição do modelo.
• B. mede o quanto o modelo linear é apropriado.
• C. mede a magnitude da inclinação da reta de regressão.
• D. sua magnitude não depende do intervalo de variação do regressor X.
• E. mede a proporção da variabilidade da variável resposta (Y) que é explicada pelo regressor X.

Considere o modelo de regressão linear múltipla. São indícios de multicolinearidade, EXCETO:

• A. Padrão não aleatório no gráfico de resíduos versus valores ajustados.
• B. Estatística F da ANOVA significante e estatísticas individuais t não significantes.
• C. Grandes alterações nas estimativas dos coeficientes de regressão quando uma ou mais observações são excluídas do banco de dados.
• D. Grandes alterações nas estimativas dos coeficientes de regressão quando uma variável explicativa é adicionada ou retirada do modelo.
• E. Coeficientes de regressão com magnitudes muito diferentes ou com sinais opostos àqueles esperados a partir de considerações teóricas.

• A. regressão linear.
• B. regressão cúbica.
• C. regressão quadrática.
• D. regressão exponencial.
• E. regressão logarítmica.

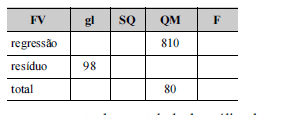
O quadro acima mostra parte de uma tabela de análise de variância (ANOVA), que resultou da regressão linear simples do tempo que um usuário permanece conectado à Internet 3G — Y, em minutos — sobre a renda — X — declarada por esse usuário. Os dados utilizados nesse ajuste pelo método de mínimos quadrados ordinários foram selecionados por amostragem aleatória simples de um cadastro de usuários. Com base nessas informações e no quadro apresentado, julgue os itens seguintes acerca dos conceitos de análise de regressão, correlação e amostragem.

O método de mínimos quadrados ordinários para a estimação dos coeficientes do modelo requer a suposição de normalidade dos resíduos.

• C. Certo
• E. Errado

Um modelo de regressão linear múltipla, com intercepto, consiste de uma variável dependente, 3 variáveis explicativas e com base em 12 observações. As estimativas dos parâmetros do modelo foram obtidas pelo método dos mínimos quadrados e o valor encontrado da estatística F (F calculado) utilizado para testar a existência da regressão foi igual a 14. O coeficiente de explicação (R²), definido como sendo o resultado da divisão da variação explicada pela variação total, é, em %, igual a

• A.

  80,0.

• B.

  76,8.

• C.

  78,0.

• D.

  72,0.

• E.

  84,0.

Um diagrama de correlação ou de dispersão fornece uma representação da relação entre duas variáveis, verificando a maior ou menor (ou não se verificando) dependência de uma variável para outra. Pelos pontos obtidos de cada uma dessas variáveis, no diagrama de dispersão, é possível traçar o seguinte modelo matemático:

• A.

  parábola.

• B.

  curva gaussiana.

• C.

  distribuição binomial de Newton.

• D.

  distribuição de Poisson.

• E.

  reta de regressão.