Questões de Estatística da Centro de Seleção e de Promoção de Eventos UnB (CESPE)

A tabela acima mostra a distribuição de probabilidade conjunta da quantidade diária X de animais domésticos vendidos e a quantidade Y de ração vendida (em kg) por dia em determinada loja. Com base nessa tabela e nos conceitos de distribuição conjunta, julgue os itens seguintes.

O desvio padrão de X é inferior ao valor da média de X.

• C. Certo
• E. Errado

Julgue os itens seguintes, acerca de probabilidades.

Considere que, para determinada companhia telefônica, as ligações que ultrapassarem 1 minuto sejam tarifadas em R$ 1,00 e as ligações de tempo inferior a 1 minuto sejam tarifadas em R$ 0,80. Nesse caso, se o número X de ligações efetuadas seguir uma distribuição de Poisson com média igual a 500 ligações por minuto e se a probabilidade de uma ligação durar mais de 1 minuto for igual a 0,10, então a arrecadação esperada em cada minuto será igual ou inferior a R$ 50,00.

• C. Certo
• E. Errado

Com relação a problemas aritméticos e matriciais, cada um dos próximos itens apresenta uma situação hipotética, seguida de uma assertiva a ser julgada.

Se, em um município, as seções eleitorais X, Y e Z têm, juntas, 1.500 eleitores; os tempos médios de votação nessas seções são 1 minuto e 30 segundos, 2 minutos e 1 minuto por eleitor, respectivamente; o tempo médio de votação nas três seções é de 2.175 minutos; e o número de eleitores da seção Y é igual à metade da soma do número de eleitores das seções X e Z, então, nesse caso, a seção eleitoral que tem o maior número de eleitores é a X.

• C. Certo
• E. Errado

Julgue os itens subsecutivos, relativos a planejamento e organização de pesquisas.

As diferenças entre população-alvo e população acessível devem ser avaliadas no processo de amostragem e na consequente inferência.

• C. Certo
• E. Errado

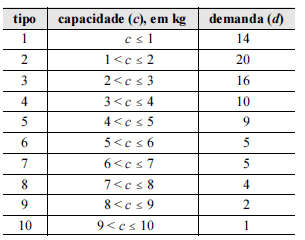
Considere que determinado fabricante classifique suas embalagens de acordo com a capacidade de armazenamento unitário (c), em kg, de determinado produto — por exemplo, a embalagem do tipo 10 permite armazenar mais de 9 e até 10 kg do produto. Com base nessas informações e na tabela acima, que mostra a distribuição dos dez tipos de embalagens e a demanda observada em março de 2011 para cada tipo, julgue os itens que se seguem.

A capacidade média das embalagens demandadas foi superior a 4 kg.

• C. Certo
• E. Errado

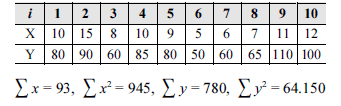
A fim de planejar o orçamento de uma grande empresa para o próximo ano, um analista selecionou uma amostra aleatória de 10 produtos (i) das empresas filiais e anotou as despesas (X) e os faturamentos (Y) totais decorrentes desses produtos (em R$ milhões). Os resultados por ele obtidos são mostrados na tabela acima.

Com base nessas informações, julgue os itens subsecutivos.

A média das despesas X por produto foi igual a R$ 9,3 milhões.

• C. Certo
• E. Errado

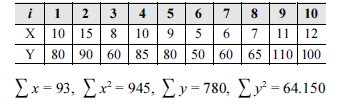
A fim de planejar o orçamento de uma grande empresa para o próximo ano, um analista selecionou uma amostra aleatória de 10 produtos (i) das empresas filiais e anotou as despesas (X) e os faturamentos (Y) totais decorrentes desses produtos (em R$ milhões). Os resultados por ele obtidos são mostrados na tabela acima.

Com base nessas informações, julgue os itens subsecutivos.

A estimativa do faturamento médio por produto foi superior a 8 vezes o valor da despesa média por produto.

• C. Certo
• E. Errado

Considerando que, em determinada população, a probabilidade de um indivíduo recém-nascido sobreviver pelo menos até a idade x, medida em anos, é dada pela função de sobrevivência S(x)= 1 – -x²/10.000, julgue os itens a seguir.

Nessa população, a expectativa de vida de um indivíduo ao nascer é superior a 70 anos.

• C. Certo
• E. Errado

Considerando as desigualdades usuais em teoria de probabilidades, julgue os próximos itens.

Suponha que X seja uma variável aleatória com esperança finita. Isto garante que a média da variável aleatória Y = exp(X) também será finita.

• C. Certo
• E. Errado

– 5 – Com relação às medidas de dispersão, considerando que  representa a média aritmética de um conjunto de dados {X₁, X₂, ..., X_n}, julgue os itens que se seguem.

A função a seguir não é uma medida de dispersão válida.

• C. Certo
• E. Errado