Questões de Estatística da Centro de Seleção e de Promoção de Eventos UnB (CESPE)

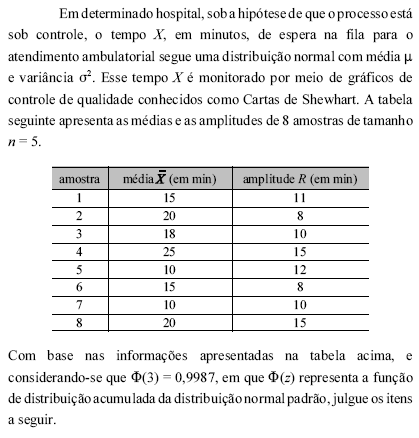
O número de pacientes (X) recebidos em um hospital para o atendimento ambulatorial e o número (Y) de pacientes recebidos no mesmo hospital para o atendimento de emergência seguem processos de Poisson homogêneos com médias, respectivamente, iguais a 10 pacientes/dia e 5 pacientes/dia. As variáveis aleatórias X e Y são independentes. Em média, 5% dos pacientes do atendimento ambulatorial são internados, enquanto 80% dos pacientes do atendimento emergencial são internados. Considerando que a decisão pela internação ou não internação seja feita no instante que o paciente chega ao hospital e que Z representa o número diário de pacientes internados nesse hospital, julgue os seguintes itens.

Considerando-se que cada dia possui 24 horas, o tempo médio de chegada entre dois pacientes consecutivos para o atendimento ambulatorial é inferior a 2 horas.

• C. Certo
• E. Errado

Texto para as questões de 26 a 29

A figura acima apresenta a evolução temporal da quantidade de carvão vegetal - em toneladas - produzida no Brasil entre os anos 1990 e 2006. Ao longo desse período, a produção anual média de carvão vegetal foi de 2,4 milhões de toneladas/ano, o desvio padrão amostral foi de 470 mil toneladas e a correlação linear entre a produção e o ano foi igual a 0,15.

Quanto à utilização das técnicas de análise de séries temporais nos dados apresentados no texto,

• A.

  a evolução temporal da quantidade de carvão vegetal - em toneladas - produzida no Brasil entre os anos 1990 e 2006 é uma série sazonal.

• B.

  o método de alisamento de Holt-Winters pode ser aplicado para gerar previsões para séries temporais com tendência de crescimento linear.

• C.

  o filtro de Kalman é um algoritmo para o cálculo de previsões, mas a sua utilização não é recomendada para séries não estacionárias.

• D.

  o algoritmo de Durbin-Levinson é um algoritmo não recursivo para o cálculo de previsões de máxima verossimilhança tanto para as séries temporais estacionárias como para as que não são estacionárias.

A distribuição de 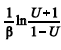T pode ser obtida a partir da transformação _, em que U segue uma  distribuição uniforme no intervalo (0,1).

• C. Certo
• E. Errado

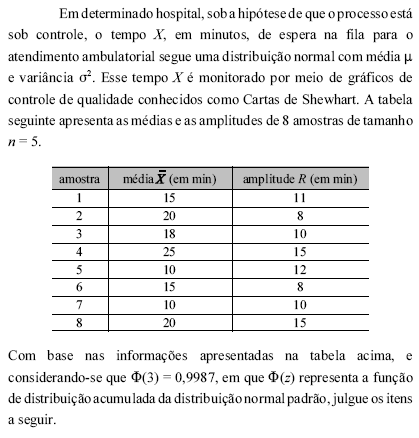
Os limites de controle 6 sigma para a carta 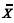são equivalentes aos limites de confiança de 99,87% para a média :, sob a hipótese de que o processo está sob controle.

• C. Certo
• E. Errado

Considere que X(t) represente o número de postos de trabalho disponíveis no instante t e que Y(t) represente o número de trabalhadores disponíveis no instante t para a ocupação desses postos. Considere também que X(t) e Y(t) sejam independentes e sigam processos estocásticos de Poisson. Nesse modelo, os valores esperados de X(t) e Y(t) são, respectivamente, iguais a 5t e 6t, em que t é um número real não-negativo, e o excesso de trabalhadores em relação à quantidade de postos disponíveis é definido pela diferença D(t) = Y(t) - X(t). Com base nessas definições, julgue os itens a seguir.

O processo estocástico D(t) possui incrementos independentes.

• C. Certo
• E. Errado

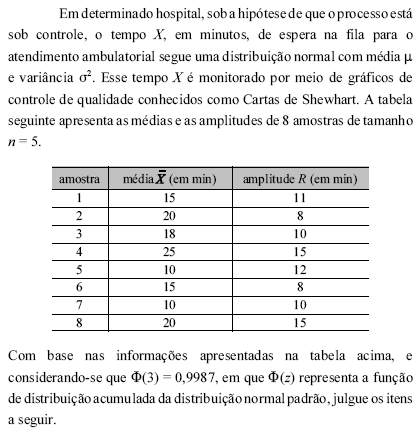
Considere que os limites de controle para a carta 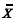 são construídos de modo que a probabilidade de que um ponto caia além desses limites, mesmo que o processo esteja sob controle, seja igual a 0,005. Nesse caso, o ARL 0 (average run length de um processo sob controle) será inferior a 350.

• C. Certo
• E. Errado

Considerando as informações do texto, julgue os itens subseqüentes.

A variável X forma uma série estatística denominada série temporal.

• C. Certo
• E. Errado

Considere que X(t) represente o número de postos de trabalho disponíveis no instante t e que Y(t) represente o número de trabalhadores disponíveis no instante t para a ocupação desses postos. Considere também que X(t) e Y(t) sejam independentes e sigam processos estocásticos de Poisson. Nesse modelo, os valores esperados de X(t) e Y(t) são, respectivamente, iguais a 5t e 6t, em que t é um número real não-negativo, e o excesso de trabalhadores em relação à quantidade de postos disponíveis é definido pela diferença D(t) = Y(t) - X(t). Com base nessas definições, julgue os itens a seguir.

A diferença entre X(t) e Y(t) resulta em um processo estocástico estacionário.

• C. Certo
• E. Errado

Considere que a probabilidade de se detectar uma mudança na média do processo seja igual a 0,25. Nessa situação, o número esperado de amostras até que a mudança seja detectada é inferior a 2.

• C. Certo
• E. Errado

Considere-se o modelo de séries temporais em tempo discreto na forma 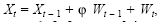em que t representa o tempo, 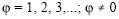é o coeficiente do modelo e Wt representa um processo de choques aleatórios com média zero e variância 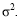Com base nessas informações, julgue os itens seguintes, acerca da primeira diferença Xt - Xt - 1.

Essa diferença é uma série temporal fracamente estacionária.

• C. Certo
• E. Errado