Questões de Estatística da Centro de Seleção e de Promoção de Eventos UnB (CESPE)

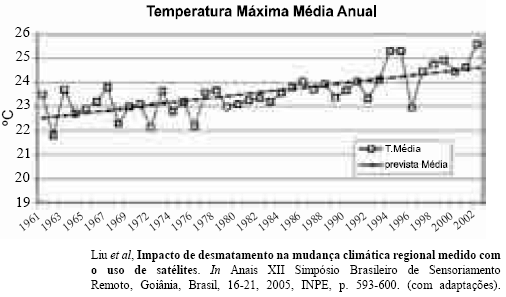
A figura acima apresenta os resultados de um estudo acerca da evolução temporal da temperatura máxima média anual — Y — de 1961 a 2002 e sua relação com o desmatamento em uma área da região amazônica. A tendência de crescimento linear foi obtida pelo método de mínimos quadrados ordinários. De acordo com esse modelo de regressão linear simples, os valores ajustados para a temperatura Y em 1961 e 2002 foram iguais a 22,5 ºC e 24,5 ºC, respectivamente, e o coeficiente de determinação (R²) foi igual a 0,72.

Com base nas informações apresentadas, julgue os itens subseqüentes.

A série temporal é estacionária.

• C. Certo
• E. Errado

Considere que um processo estocástico de Wiener seja representado por 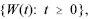 com Var[W(t)] = 0,25t e a transformação X(t) = [W(t)]². Nessa situação, julgue os itens que se seguem.

Considere-se um processo de choques aleatórios (ruído branco ou white noise) representado por 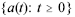com E[a(t)] = 0, Var[a(t)] = 0,25 e independente de {W(t)}. Nessa situação, o processo H(t) = W(t) - W(t - 1) + a(t), em que t > 1, é um processo estacionário em torno de zero.

• C. Certo
• E. Errado

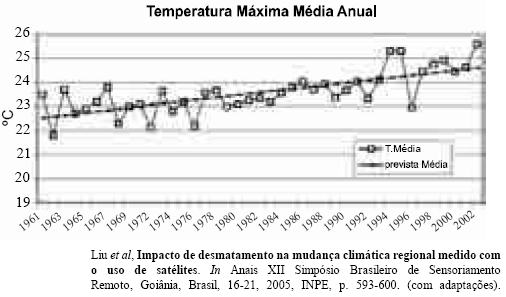
A figura acima apresenta os resultados de um estudo acerca da evolução temporal da temperatura máxima média anual — Y — de 1961 a 2002 e sua relação com o desmatamento em uma área da região amazônica. A tendência de crescimento linear foi obtida pelo método de mínimos quadrados ordinários. De acordo com esse modelo de regressão linear simples, os valores ajustados para a temperatura Y em 1961 e 2002 foram iguais a 22,5 ºC e 24,5 ºC, respectivamente, e o coeficiente de determinação (R²) foi igual a 0,72.

Com base nas informações apresentadas, julgue os itens subseqüentes.

A tendência linear apresentada na figura pode ser obtida pelo método do alisamento exponencial simples aplicado à série temporal Y.

• C. Certo
• E. Errado

A forma quadrática 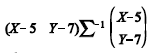 segue uma distribuição qui-quadrado.

• C. Certo
• E. Errado

Considere uma amostra aleatória simples X₁, X₂, ..., X_n de uma distribuição com função de distribuição acumulada F(x), em que x é um número real. Para essa amostra, a função de distribuição acumulada empírica é definida como 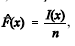 , em que I(x) é o número de elementos na amostra que são iguais ou inferiores a x. Com referência a essa situação, julgue os seguintes itens.

A estatística do teste de Kolmogorov-Smirnov definida por 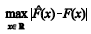 é assintoticamente normal.

• C. Certo
• E. Errado

A autocorrelação entre X_t e X_{t - 6} é inferior a ß⁴.

• C. Certo
• E. Errado

        Um analista deseja testar a hipótese nula — H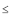₀ — de que o tempo T, referido no texto, segue uma distribuição exponencial. Sob essa hipótese, os percentuais acumulados esperados são aproximadamente iguais a 22%, 39% e 78%, respectivamente, para os intervalos de classe T  0,5 ano, T  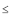1 ano e T  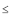3 anos.

 A partir dessas informações, julgue os itens subseqüentes.

O teste qui-quadrado de aderência consiste na comparação do percentual de casos ocorridos em determinado intervalo de classe com o respectivo percentual esperado de casos, na situação em que a hipótese nula for verdadeira.

• C. Certo
• E. Errado

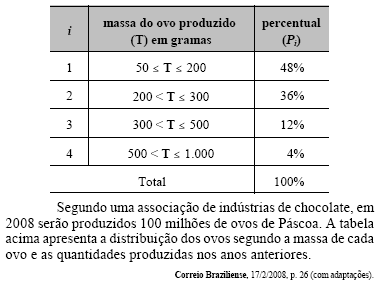
Com base nessas informações, julgue os itens subseqüentes.

A produção, em toneladas, esperada para o ano de 2008 é superior a 22 mil e inferior a 23 mil ovos de Páscoa.

• C. Certo
• E. Errado

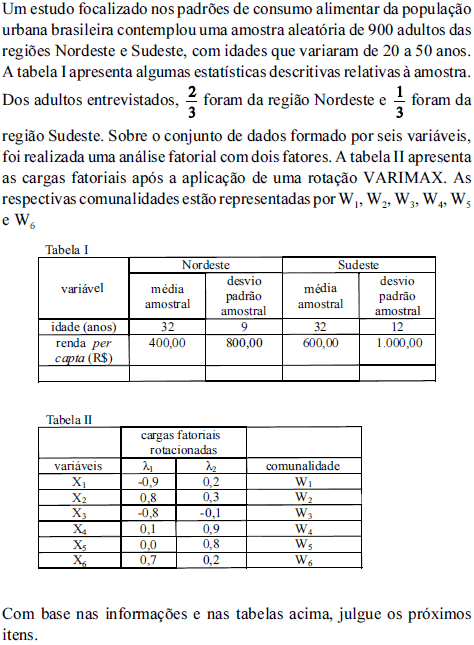
O percentual da variação total explicada pelos dois fatores é superior a 65% da variação total.

• C. Certo
• E. Errado

Um dos principais objetivos da epidemiologia é proporcionar dados essenciais para o planejamento, execução e avaliação das ações de prevenção, controle e tratamento das doenças, bem como para estabelecer prioridades. Nesse contexto, diferentes tipos de indicadores são gerados. Acerca de alguns desses indicadores, julgue os itens a seguir.

Distribuição é o estudo da variabilidade de freqüência das doenças de ocorrência em massa, em função de uma única variável.

• C. Certo
• E. Errado