Questões de Estatística da Centro de Seleção e de Promoção de Eventos UnB (CESPE)
Lista completa de Questões de Estatística da Centro de Seleção e de Promoção de Eventos UnB (CESPE) para resolução totalmente grátis. Selecione os assuntos no filtro de questões e comece a resolver exercícios.
Estatística - Estimação e Intervalo de Confiança - Centro de Seleção e de Promoção de Eventos UnB (CESPE) - 2014

Considerando as informações apresentadas no texto acima e supondo que um analista pretenda elaborar um plano amostral por meio de uma amostra aleatória simples sem reposição das linhas ativas na telefonia móvel com o objetivo de estimar a proporção de ligações não completas em junho de 2014, julgue os itens a seguir.
O tamanho amostral máximo necessário para se estimar a proporção de ligações não completas com margem de erro de 5% e nível de 95% de confiança é superior a 3.850 linhas ativas.- C. Certo
- E. Errado

A respeito da amostra apresentada no texto, em relação à quantidade de Escherichia coli, é correto afirmar que
- A.
a média é igual a 5, a mediana é igual a 5,5 e a variância é igual a 34/9.
- B.
a média é igual a 5, a mediana é igual a 5,5 e a variância é igual a 34/10.
- C.
a média é igual a 5, a mediana é igual a 5 e a variância é igual a 34/9.
- D.
a média é igual a 5,5, a mediana é igual a 5 e a variância é igual a 34/10.
- E.
a média é igual a 5, a mediana é igual a 5,5 e a variância é igual a 6.

O coeficiente de correlação de Pearson entre a quantidade de Escherichia coli (em UFC/mL) e o tempo de estocagem (em horas) foi estimado em 0,73. Observando-se apenas o valor desse coeficiente, é correto afirmar que
- A.
as variáveis quantidade de Escherichia coli e tempo de estocagem são independentes.
- B.
existe uma relação negativa entre a quantidade de Escherichia coli e o tempo de estocagem.
- C.
existe uma relação positiva entre a quantidade de Escherichia coli e o tempo de estocagem.
- D.
o tempo de estocagem é responsável pela quantidade de Escherichia coli presente na amostra.
- E.
o tempo de estocagem depende da quantidade de Escherichia coli.

Um dos frascos do xarope, na referida amostra, foi coletada aleatoriamente e a quantidade de Escherichia coli foi anotada. Outra unidade foi selecionada por apresentar turvação e verificou-se tratar do produto com maior quantidade de Escherichia coli. Procedeu-se então à coleta aleatória de uma terceira unidade. Na primeira seleção, considera-se X a probabilidade de que a unidade do xarope selecionada tenha quantidade de Escherichia coli maior do que 5 UFC/mL. Já na coleta da terceira unidade, considera-se Y a probabilidade de que essa amostra apresente quantidade de Escherichia coli menor do que 5 UFC/mL. Verifica-se que a primeira unidade selecionada apresentou quantidade de Escherichia coli igual a 6 UFC/mL.
Sabendo-se que, no processo de coleta aleatória, todas as unidades do xarope possuem a mesma probabilidade de serem selecionadas, então, os valores de X e Y são, respectivamente- A.
50% e 44%.
- B.
50% e 50%.
- C.
60% e 40%.
- D.
50% e 40%.
- E.
44% e 50%.
É sabido que aproximadamente 95% dos valores de uma variável aleatória que segue uma distribuição normal encontram-se entre -1,96 e 1,96 desvios padrão abaixo e acima, respectivamente, da média da distribuição. Sabe-se, também, que o tempo de vida de um determinado parasita ao ar livre segue uma distribuição normal com média igual a dez horas e desvio padrão igual a 1 hora. Entretanto, quando na presença de um fármaco específico, o tempo de vida do parasita continua seguindo uma distribuição normal, porém com média igual a uma hora e desvio padrão de 0,5 hora. Ao ar livre, espera-se que após 11,96 horas, a porcentagem de parasitas vivos seja de X%. Já na presença do fármaco, espera-se uma porcentagem de Y% de parasitas vivos após uma hora de exposição. Os valores de X% e Y% são, respectivamente
- A.
7,5% e 95%.
- B.
5% e 50%.
- C.
2,5% e 47,5%.
- D.
2,5% e 50%.
- E.
5% e 47,5%.
Estatística - Correlação e Regressão Linear - Centro de Seleção e de Promoção de Eventos UnB (CESPE) - 2013

- A.
Como o valor do coeficiente da variável r é bastante superior aos demais coeficientes, essa variável é a mais relevante na explicação científica da quantidade de infectados.
- B.
Como o valor do R-quadrado da equação de regressão é elevado, a quantidade de pessoas infectadas em um dado ano depende das variáveis estudadas.
- C.
Apesar do coeficiente da variável r ser significativo ao nível de significância de 1%, a causalidade entre a quantidade de infectados e a quantidade de repelentes vendida pode ser questionada.
- D.
Como o valor-p das variáveis da e $ foram superiores a 0,7; a eliminação das mesmas da equação de regressão irá aumentar o seu R-quadrado.
- E.
Como o valor da constante da equação de regressão é elevado, quando comparado com os valores dos coeficientes, pouco se pode fazer para a redução da quantidade de casos de dengue abaixo de tal valor.

A figura acima apresenta os diagramas esquemáticos (box-plot) referentes às distribuições das eficiências (W) proporcionadas por três diferentes tipos de células fotovoltaicas. Nesses diagramas, o ponto no interior de cada caixa (box) refere-se à média amostral da distribuição. Com base nessas informações, julgue os itens que se seguem.
Em cada box-plot, a caixa ou a área retangular do diagrama corresponde a 75% da distribuição das eficiências.
- C. Certo
- E. Errado

A figura acima apresenta os diagramas esquemáticos (box-plot) referentes às distribuições das eficiências (W) proporcionadas por três diferentes tipos de células fotovoltaicas. Nesses diagramas, o ponto no interior de cada caixa (box) refere-se à média amostral da distribuição. Com base nessas informações, julgue os itens que se seguem.
Os diagramas correspondentes aos tipos 1 e 3 apresentam valores atípicos (ou outliers) na cauda inferior, o que sugere que ambas as distribuições possuem assimetria negativa.
- C. Certo
- E. Errado

A figura acima apresenta os diagramas esquemáticos (box-plot) referentes às distribuições das eficiências (W) proporcionadas por três diferentes tipos de células fotovoltaicas. Nesses diagramas, o ponto no interior de cada caixa (box) refere-se à média amostral da distribuição. Com base nessas informações, julgue os itens que se seguem.
O primeiro quartil de cada distribuição é superior a 3,75 e inferior a 4,25.
- C. Certo
- E. Errado
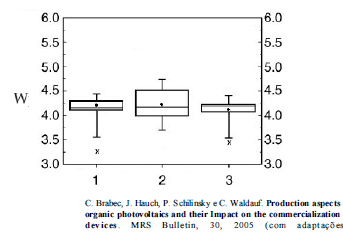
A figura acima apresenta os diagramas esquemáticos (box-plot) referentes às distribuições das eficiências (W) proporcionadas por três diferentes tipos de células fotovoltaicas. Nesses diagramas, o ponto no interior de cada caixa (box) refere-se à média amostral da distribuição. Com base nessas informações, julgue os itens que se seguem.
Em cada distribuição, o desvio padrão é inferior a 2,0.
- C. Certo
- E. Errado


