Questões de Estatística da Fundação Carlos Chagas (FCC)

Durante uma semana, observa-se a quantidade de determinadas ocorrências, esperando que diariamente ocorram 20 destes tipos de ocorrências. Para esta análise, foram levantados os seguintes dados em uma semana escolhida aleatoriamente:

O valor do qui-quadrado observado é

• A. inferior ao número de graus de liberdade do teste e H₀ não é rejeitada.
• B. inferior ao número de graus de liberdade do teste e H₀ é rejeitada.
• C. superior ao número de graus de liberdade do teste e H₀ não é rejeitada.
• D. superior ao número de graus de liberdade do teste e H₀ é rejeitada.
• E. superior ao número de graus de liberdade do teste e H₀ é rejeitada para qualquer nível de significância β tal α < β.

Considerando a equação da reta obtida pelo método dos mínimos quadrados, obtém-se que Y é igual a 24 quando X for igual a

• A. 15.
• B. 6.
• C. 16.
• D. 18.
• E. 20.

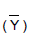O valor médio  dos 20 valores observados para Y é igual a

• A. 17,2.
• B. 30,0.
• C. 24,6.
• D. 25,8.
• E. 20,4.

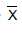O valor de S, em que  é o valor médio dos 20 valores observados para X tal que  é igual a

• A. 210,00.
• B. 270,00.
• C. 240,00.
• D. 300,00.
• E. 192,00.

Pelo quadro de análise de variância correspondente, observa-se que

• A. o coeficiente de determinação (R2), definido como sendo o resultado da divisão da variação explicada pela variação total, é igual a 80%.
• B. a variação explicada, fonte de variação devido à regressão, é igual a 240.
• C. o valor da estatística F (F calculado) utilizado para testar a existência da regressão é igual a 32.
• D. o valor da estimativa da variância do modelo teórico é igual a 10,8.
• E. a variação explicada, fonte de variação devido à regressão, tem distribuição qui-quadrado com 18 graus de liberdade.

Atenção: Para responder às questões de números 41 e 42, considere as informações abaixo.

O número de funcionários de três empresas A, B, e C, é igual a 20, 10 e 20, respectivamente. Sabe-se que dentre os funcionários de A, B e C, 40%, 20% e 25%, respectivamente, são do sexo feminino.

Três funcionários serão selecionados aleatoriamente e sem reposição dentre os funcionários que são do sexo feminino. A probabilidade de, exatamente, 2 serem da empresa C é igual a

• A. 5/17.
• B. 10/89.
• C. 20/91.
• D. 43/182.
• E. 12/45.

Atenção: Para responder às questões de números 41 e 42, considere as informações abaixo.

O número de funcionários de três empresas A, B, e C, é igual a 20, 10 e 20, respectivamente. Sabe-se que dentre os funcionários de A, B e C, 40%, 20% e 25%, respectivamente, são do sexo feminino.

Quatro funcionários serão selecionados, aleatoriamente e com reposição, dentre os que são da empresa A. A probabilidade de, exatamente, 2 serem do sexo masculino é, em %, igual a

• A. 35,16.
• B. 28,34.
• C. 38,12.
• D. 24,72.
• E. 34,56.

A probabilidade de uma criança no ano A e da faixa etária B, contrair coqueluche é 0,2% se ela for vacinada e 1% se ela não for vacinada. Sabe-se que 90% da população de crianças no ano A e da faixa etária B foram vacinadas. Se uma criança, da faixa etária e do ano citados contrair coqueluche, a probabilidade de ela ter sido vacinada é igual a

• A. 9/14.
• B. 11/8.
• C. 9/28.
• D. 5/14.
• E. 10/28.

Uma montadora fabrica veículos 1.0 nas cores prata, preta, vermelha e branca. Suponha que dos veículos 1.0 produzidos, 40%, 30%, 20% e 10%, respectivamente, sejam nas cores prata, preta, vermelha e branca. Seleciona-se, ao acaso e com reposição, 6 compradores de tais veículos. A probabilidade de, nessa amostra, respectivamente, 2, 2, 1 e 1, compradores terem escolhido as cores prata, preta, vermelha e branca, é, em %, dada por

• A. 2,534.
• B. 5,184.
• C. 3,258.
• D. 8,450.
• E. 6,820.

A variável aleatória contínua X tem distribuição uniforme no intervalo [a, b]. Sabe-se que a média de X é 3 e que o primeiro quartil de X é 1. Nessas condições, a variância de X é igual a

• A. 16/3.
• B. 25/12.
• C. 18/7.
• D. 12/5.
• E. 4/3.