Questões de Estatística da Núcleo de Computação Eletrônica UFRJ (NCE)

Ordenados os elementos da amostra, x é o valor (pertencente ou não à amostra) que a divide ao meio, isto é, 50% dos elementos da amostra são menores ou iguais a x e os outros 50% são maiores ou iguais a x.

Para a sua determinação utiliza-se a seguinte regra, depois de ordenada a amostra de n elementos:

Se n é ímpar, x é o elemento médio.

Se n é par, x a semi-soma dos dois elementos médios.

Trata-se como regra geral:

• A.

  da média;

• B.

  da moda;

• C.

  da mediana;

• D.

  do desvio Padrão;

• E.

  do t de “Student”.

O ajuste de uma reta de regressão linear se faz por meio do método de:

• A.

  máxima verossimilhança;

• B.

  mínimos quadrados;

• C.

  componentes principais;

• D.

  qui-quadrados ponderados;

• E.

  Fisher.

Uma variável aleatória X tem função de densidade de probabilidade dada por:

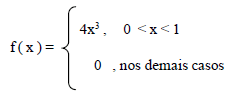
A média de X é igual a:

• A.

  0,4

• B.

  0,5

• C.

  0,6

• D.

  0,7

• E.

  0,8

A tabela abaixo informa preços (em mil dólares) praticados pelos Estados Unidos e por alguns países asiáticos no procedimento médico de substituição de válvula cardíaca:

Considerando-se os dados da tabela, pode-se afirmar que a média de preços incluindo os Estados Unidos é maior que a média de preços excluindo os Estados Unidos em aproximadamente:

• A. 4vezes;
• B. 5vezes;
• C. 6vezes;
• D. 15vezes;
• E. 16vezes;

A tabela a seguir informa o tempo que cada uma de 5 funcionárias gastou para realizar o mesmo serviço.

A funcionária que levou mais tempo para realizar o serviço foi:

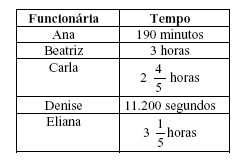
• A. Ana;
• B. Beatriz;
• C. Carla;
• D. Denise;
• E. Eliana.

Uma amostra aleatória simples, de tamanho 4, de uma densidade normal com média  apresentou os seguintes valores:

2,0      4,0       3,0       3,0

 

O problema é testar . O valor-p (significância) associado à estatística de teste usual é tal que:

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

Se X é um vetor, com p componentes, que tem distribuição normal multivariada com vetor de médias  e matriz de covariâncias , e se C é uma matriz p×p não singular, com transposta C', então Y = CX tem distribuição normal multivariada com vetor de médias C e matriz de covariâncias:

• A.

  C'S;

• B.

  CSC';

• C.

  C^-1SC;

• D.

  C'SC;

• E.

  CS^-1C'.

Uma amostra aleatória simples X₁, X₂, ... , X_n, de tamanho n, será obtida de uma população descrita por uma densidade normal com média 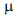 e variância . Se X representa a média amostral e se 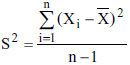  , então a seguinte variável tem distribuição qui-quadrado com n – 1 graus de liberdade:

• A.

  S²

• B.
• C.
• D.
• E. nS²

Para testar se as proporções populacionais referentes à classificação dos elementos populacionais em quatro categorias A, B, C e D são iguais a 20%, 30%, 30% e 20%, uma amostra aleatória simples de tamanho 400 foi obtida e as freqüências observadas foram: classe A: 80, classe B: 100, classe C: 120, classe D: 100. O valor da estatística qui-quadrado usual para esses dados é aproximadamente igual a:

• A.

  2,64;

• B.

  4,06;

• C.

  5,28;

• D.

  6,78;

• E.

  8,33.

Com o objetivo de se testar independência entre dois atributos, a tabela de contingências 3 X 2 a seguir foi observada:

A freqüência esperada sob a hipótese de independência na célula ( 2, 2 ) é igual a:

• A.

  320;

• B.

  360;

• C.

  440;

• D.

  460;

• E.

  520.