Questões de Matemática
Lista completa de Questões de Matemática para resolução totalmente grátis. Selecione os assuntos no filtro de questões e comece a resolver exercícios.
Teorema de Pitágoras
O teorema de Pitágoras é uma relação matemática entre os comprimentos dos lados de qualquer triângulo retângulo. Na geometria euclidiana, o teorema afirma que em qualquer triângulo retângulo, o quadrado do comprimento da hipotenusa é igual à soma dos quadrados dos comprimentos dos catetos.
Por definição, a hipotenusa é o lado oposto ao ângulo reto, e os catetos são os dois lados que o formam. Assim, o teorema de Pitágoras também pode ser enunciado como uma relação entre áreas: em qualquer triângulo retângulo, a área do quadrado cujo lado é a hipotenusa é igual à soma das áreas dos quadrados cujos lados são os catetos.
Para ambos os enunciados anteriormente mencionados, pode-se equacionar: c² = b² + a², onde c representa o comprimento da hipotenusa, e a e b representam os comprimentos dos outros dois lados.
A demonstração do teorema de Pitágoras utilizando a comparação de áreas pode ser feita da seguinte forma:
1. Desenha-se um quadrado de lado b + a;
2. Subdivide-se este quadrado em quatro retângulos, sendo dois deles quadrados de lados, respectivamente, a e b: Traça-se dois segmentos de reta paralelos a dois lados consecutivos do quadrado, sendo cada um deles interno ao quadrado e com o mesmo comprimento que o lado do quadrado;
3. Divide-se cada um destes dois retângulos em dois triângulos retângulos, traçando-se as diagonais. Chama-se c o comprimento de cada diagonal;
4. A área da região que resta ao retirar-se os quatro triângulos retângulos é igual a b² + a²;
5. Desenha-se agora o mesmo quadrado de lado b + a, mas coloca-se os quatro triângulos retângulos noutra posição dentro do quadrado: a posição que deixa desocupada uma região que é um quadrado de lado c.
6. Assim, a área da região formada quando os quatro triângulos retângulos são retirados é igual a c².
Como b² + a² representa a área do quadrado maior subtraída da soma das áreas dos triângulos retângulos, e c² representa a mesma área, então b² + a² = c². Ou seja: num triângulo retângulo o quadrado da hipotenusa é igual à soma dos quadrados dos catetos.
Adaptado. Disponível em: https://bit.ly/2QiNr3C
Leia o texto 'Teorema de Pitágoras' e, em seguida, analise as afirmativas abaixo:
I. De acordo com o texto, na geometria euclidiana, o teorema de Pitágoras afirma que, em qualquer triângulo retângulo, o quadrado do comprimento da hipotenusa é igual à soma dos quadrados dos comprimentos dos catetos.
II. O teorema de Pitágoras é uma relação matemática entre os comprimentos dos lados de qualquer triângulo isósceles, de acordo com o texto.
III. O 6º passo para a demonstração do teorema de Pitágoras utilizando a comparação de áreas, de acordo com o texto, é verificar que a área da região formada quando os quatro triângulos retângulos são retirados é igual a c², de acordo com o texto.
Marque a alternativa CORRETA:
I. De acordo com o texto, na geometria euclidiana, o teorema de Pitágoras afirma que, em qualquer triângulo retângulo, o quadrado do comprimento da hipotenusa é igual à soma dos quadrados dos comprimentos dos catetos.
II. O teorema de Pitágoras é uma relação matemática entre os comprimentos dos lados de qualquer triângulo isósceles, de acordo com o texto.
III. O 6º passo para a demonstração do teorema de Pitágoras utilizando a comparação de áreas, de acordo com o texto, é verificar que a área da região formada quando os quatro triângulos retângulos são retirados é igual a c², de acordo com o texto.
Marque a alternativa CORRETA:
-
A) Nenhuma afirmativa está correta.
B) Apenas uma afirmativa está correta.
C) Apenas duas afirmativas estão corretas.
D) Todas as afirmativas estão corretas.
Analise as afirmativas a seguir:
I. Os preços do produto X em três diferentes lojas são, respectivamente: R$ 6,50, R$ 6,90 e R$ 7,60. Assim, considerando exclusivamente as informações apresentadas, é correto afirmar que o preço médio desse produto, nos estabelecimentos considerados, é maior que R$ 6,92 e menor que R$ 7,16.
II. Na sala de espera de um pediatra há quatro crianças que pesam, respectivamente: 15 quilos, 26 quilos, 32 quilos e 49 quilos. Assim, é correto afirmar que o peso médio dessas crianças é maior que 29,2 quilos.
III. A montagem de uma máquina foi realizada através de 4 etapas sequenciais que duraram, respectivamente: 65 minutos, 33 minutos, 63 minutos e 16 minutos. Assim, considerando exclusivamente as informações apresentadas, é correto afirmar que o tempo total dessa montagem foi inferior a 3,2 horas.
Marque a alternativa CORRETA:
I. Os preços do produto X em três diferentes lojas são, respectivamente: R$ 6,50, R$ 6,90 e R$ 7,60. Assim, considerando exclusivamente as informações apresentadas, é correto afirmar que o preço médio desse produto, nos estabelecimentos considerados, é maior que R$ 6,92 e menor que R$ 7,16.
II. Na sala de espera de um pediatra há quatro crianças que pesam, respectivamente: 15 quilos, 26 quilos, 32 quilos e 49 quilos. Assim, é correto afirmar que o peso médio dessas crianças é maior que 29,2 quilos.
III. A montagem de uma máquina foi realizada através de 4 etapas sequenciais que duraram, respectivamente: 65 minutos, 33 minutos, 63 minutos e 16 minutos. Assim, considerando exclusivamente as informações apresentadas, é correto afirmar que o tempo total dessa montagem foi inferior a 3,2 horas.
Marque a alternativa CORRETA:
-
A) Nenhuma afirmativa está correta.
B) Apenas uma afirmativa está correta.
C) Apenas duas afirmativas estão corretas.
D) Todas as afirmativas estão corretas.
Faltam 7 semanas e 4 dias para Pedro completar 15 anos. Quantos dias faltam para o aniversário de Pedro?
-
A) 11 dias.
B) 18 dias.
C) 49 dias.
D) 53 dias.
Assinale a alternativa que apresenta o resultado da seguinte operação:
(d + g).(j + k)
-
A) d² + 2dg + 2dj + k²
B) dj + dk + gj + gk
C) dj² + dk² + gj² + gk²
D) dg + jk + dj + dk + gj + gk
E) dg² + jk + dj + dk + gj + gk²
Das 220 pessoas que trabalham em uma indústria, sabe-se que 40% falam inglês e 60% são do sexo masculino. Se 25% do número de mulheres falam inglês, a probabilidade de selecionar um funcionário dessa empresa que seja do sexo masculino e que não fale inglês é de
-
A) 5/6.
B) 5/12.
C) 1/2.
D) 3/10.
E) 9/20.
Matemática - Análise de Tabelas e Gráficos - Centro de Seleção e de Promoção de Eventos UnB (CESPE) - 2020
O gráfico a seguir mostra o percentual de preenchimento do reservatório de água de uma escola a cada hora do dia, das 6 horas da manhã até as 18 horas. Ao longo desse período, a água vai sendo consumida pelos alunos e funcionários, não havendo consumo de água em nenhum outro momento. Sabe-se que esse reservatório é abastecido uma única vez ao dia, durante 3 horas seguidas.
Com base nessas informações, é correto afirmar que esse reservatório é abastecido
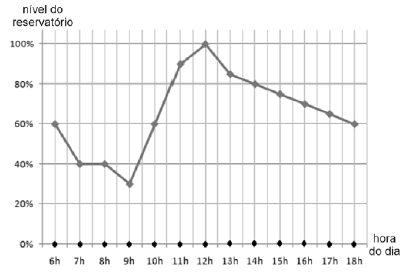
Com base nessas informações, é correto afirmar que esse reservatório é abastecido
-
A) entre 6 horas e 9 horas.
B) entre 9 horas e 12 horas.
C) entre 12 horas e 15 horas.
D) entre 15 horas e 18 horas.
E) após as 18 horas.
Analise as afirmativas a seguir:
I. Um círculo com raio igual a 234 metros terá um perímetro menor que 1.512,12 metros.
II. Considerando uma gorjeta de 5% que foi paga pelo cliente, o valor final da conta de um restaurante foi igual a R$ 609. Assim, diante dos dados apresentados, é correto afirmar que o valor referente aos alimentos efetivamente consumidos, sem a gorjeta, era superior a R$ 578,33.
Marque a alternativa CORRETA:
-
A) As duas afirmativas são verdadeiras.
B) A afirmativa I é verdadeira, e a II é falsa.
C) A afirmativa II é verdadeira, e a I é falsa.
D) As duas afirmativas são falsas.
Teorema de Pitágoras
O teorema de Pitágoras é uma relação matemática entre os comprimentos dos lados de qualquer triângulo retângulo. Na geometria euclidiana, o teorema afirma que em qualquer triângulo retângulo, o quadrado do comprimento da hipotenusa é igual à soma dos quadrados dos comprimentos dos catetos.
Por definição, a hipotenusa é o lado oposto ao ângulo reto, e os catetos são os dois lados que o formam. Assim, o teorema de Pitágoras também pode ser enunciado como uma relação entre áreas: em qualquer triângulo retângulo, a área do quadrado cujo lado é a hipotenusa é igual à soma das áreas dos quadrados cujos lados são os catetos.
Para ambos os enunciados anteriormente mencionados, pode-se equacionar: c² = b² + a², onde c representa o comprimento da hipotenusa, e a e b representam os comprimentos dos outros dois lados.
A demonstração do teorema de Pitágoras utilizando a comparação de áreas pode ser feita da seguinte forma:
1. Desenha-se um quadrado de lado b + a;
2. Subdivide-se este quadrado em quatro retângulos, sendo dois deles quadrados de lados, respectivamente, a e b: Traça-se dois segmentos de reta paralelos a dois lados consecutivos do quadrado, sendo cada um deles interno ao quadrado e com o mesmo comprimento que o lado do quadrado;
3. Divide-se cada um destes dois retângulos em dois triângulos retângulos, traçando-se as diagonais. Chama-se c o comprimento de cada diagonal;
4. A área da região que resta ao retirar-se os quatro triângulos retângulos é igual a b² + a²;
5. Desenha-se agora o mesmo quadrado de lado b + a, mas coloca-se os quatro triângulos retângulos noutra posição dentro do quadrado: a posição que deixa desocupada uma região que é um quadrado de lado c.
6. Assim, a área da região formada quando os quatro triângulos retângulos são retirados é igual a c².
Como b² + a² representa a área do quadrado maior subtraída da soma das áreas dos triângulos retângulos, e c² representa a mesma área, então b² + a² = c². Ou seja: num triângulo retângulo o quadrado da hipotenusa é igual à soma dos quadrados dos catetos.
Adaptado. Disponível em: https://bit.ly/2QiNr3C
Leia o texto 'Teorema de Pitágoras' e, em seguida, analise as afirmativas abaixo:
I. No texto, o 2º passo para a demonstração do teorema de Pitágoras utilizando a comparação de áreas exige que o quadrado seja subdividido em quatro retângulos, sendo dois deles quadrados de lados, respectivamente, a e b. Assim, deve-se traçar dois segmentos de reta paralelos a dois lados consecutivos do quadrado, sendo cada um deles interno ao quadrado e com o mesmo comprimento que o lado do quadrado, de acordo com o texto.
II. O 3º passo para a demonstração do teorema de Pitágoras utilizando a comparação de áreas, de acordo com o texto, é dividir cada um dos dois retângulos em dois triângulos retângulos, traçando-se as diagonais. Nesse caso, chama-se c o comprimento de cada diagonal.
III. O 1º passo para a demonstração do teorema de Pitágoras utilizando a comparação de áreas é desenhar um cubo de lado b + a, de acordo com o texto.
Marque a alternativa CORRETA:
I. No texto, o 2º passo para a demonstração do teorema de Pitágoras utilizando a comparação de áreas exige que o quadrado seja subdividido em quatro retângulos, sendo dois deles quadrados de lados, respectivamente, a e b. Assim, deve-se traçar dois segmentos de reta paralelos a dois lados consecutivos do quadrado, sendo cada um deles interno ao quadrado e com o mesmo comprimento que o lado do quadrado, de acordo com o texto.
II. O 3º passo para a demonstração do teorema de Pitágoras utilizando a comparação de áreas, de acordo com o texto, é dividir cada um dos dois retângulos em dois triângulos retângulos, traçando-se as diagonais. Nesse caso, chama-se c o comprimento de cada diagonal.
III. O 1º passo para a demonstração do teorema de Pitágoras utilizando a comparação de áreas é desenhar um cubo de lado b + a, de acordo com o texto.
Marque a alternativa CORRETA:
-
A) Nenhuma afirmativa está correta.
B) Apenas uma afirmativa está correta.
C) Apenas duas afirmativas estão corretas.
D) Todas as afirmativas estão corretas.
Analise as afirmativas a seguir:
I. Uma rua possui 6 (seis) casas. Sabe-se que a média aritmética do número de moradores da primeira e da segunda casa é igual ao quádruplo da média aritmética do número de moradores das quatro casas seguintes. Assim, considerando exclusivamente as informações apresentadas, é correto afirmar que a razão entre o número de moradores da primeira e da segunda casa em relação ao número total de moradores dessa rua, é equivalente a 2/3.
II. Em um supermercado, um cliente gastou 50% do dinheiro que possuía com legumes. Do que sobrou, 25% foram gastos com cereais. Após concluir suas compras, esse cliente observou que ainda lhe restaram R$ 45. Com base nos dados apresentados, é correto afirmar que o cliente possuía mais de R$ 131 antes de realizar suas compras no mercado.
III. A fração 34/81 equivale à fração 3/8 ou, em número decimal, a 0,349.
Marque a alternativa CORRETA:
-
A) Nenhuma afirmativa está correta.
B) Apenas uma afirmativa está correta.
C) Apenas duas afirmativas estão corretas.
D) Todas as afirmativas estão corretas.
José deseja fazer uma cerca em sua propriedade, para isso será necessário cerca de12km de arame. Ao convertemos 12km de arrame para metros, podemos afirmar que José gastará?
-
A) 120 metros de arrame.
B) 1.200 metros de arrame.
C) 12.000 metros de arrame.
D) 120.000 metros de arrame.
O Provas e Concursos é um banco de dados de questões de concursos públicos organizadas por matéria, assunto, ano, banca organizadora, etc
