Questões de Matemática

Amanda utiliza pequenas caixas retangulares, de dimensões 20 cm por 20 cm por 4 cm, para embalar as trufas de chocolate que fabrica em sua casa. As trufas são redondas, tendo a forma de bolas (esferas) de 4 cm de diâmetro. Considerando que as caixas devem ser tampadas, a máxima quantidade de trufas que pode ser colocada em uma caixa desse tipo é igual a

• A. 32.
• B. 25.
• C. 20.
• D. 16.
• E. 12.

Admita que a regularidade observada nos cinco primeiros elementos da sequência 2, 6, 10, 14, 18, ... mantenha-se para os números seguintes. Assim, é correto afirmar que a soma dos cem primeiros números dessa sequência é:

• A. 8 500.
• B. 15 378.
• C. 5 374.
• D. 20 000.
• E. 3 780.

O foco da parábola de equação (y – 5)² = – 2 (x + 1) é o ponto:

• A.
• B.
• C.
• D.
• E.

Um laboratório de produtos farmacêuticos possui cinco geradores que mantêm o funcionamento dos equipamentos mesmo quando há falta de energia elétrica. A partir do momento em que o fornecimento de energia é interrompido, esses geradores são ativados, operando em forma de revezamento por períodos de tempo diferentes, conforme sua capacidade. A tabela mostra o sistema de revezamento nas primeiras 24 horas após a queda de energia.

O ciclo de revezamento descrito repete-se a cada 24 horas, até que a energia seja restabelecida. Suponha que o fornecimento de energia elétrica tenha sido interrompido por 15 dias seguidos. O gerador que estava em funcionamento 307 horas após a queda de energia era o gerador

• A. I.
• B. II.
• C. III.
• D. IV.
• E. V.

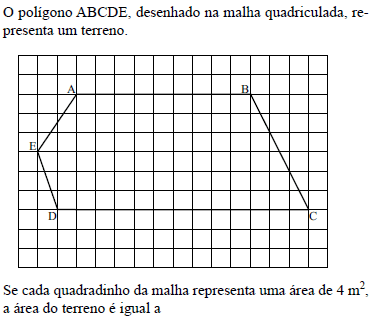
• A. 276 m².
• B. 236 m².
• C. 250 m².
• D. 180 m².
• E. 282 m².

Considere as circunferências C₁ : x² – 4y + 2x + y² – 4 = 0 e C₂ : x² – 6x + y² = – 5. Essas circunferências, em relação à posição relativa entre si, são:

• A. concêntricas
• B. tangentes
• C. coincidentes
• D. secantes
• E. paralelas

Em uma escola de 100 alunos, há três recuperações durante o ano, sendo uma em cada trimestre. Em certo ano, 55 alunos ficaram em recuperação no 1o trimestre, 48 no 2o e 40 no 3o. Somente com esses dados, é correto concluir que naquele ano, necessariamente,

• A. todos os alunos da escola ficaram em recuperação em, pelo menos, um trimestre.
• B. 40 alunos ficaram em recuperação em dois trimestres e os demais em um único.
• C. pelo menos um aluno da escola ficou em recuperação em somente dois trimestres.
• D. no mínimo 5 e no máximo 40 alunos ficaram em recuperação nos três trimestres.
• E. pelo menos 3 alunos ficaram em recuperação no 1o e também no 2o trimestre.

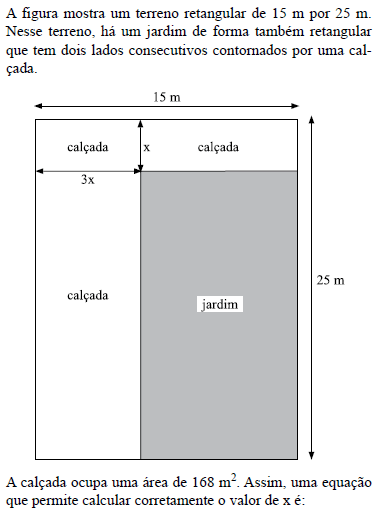
• A. x² – 30x + 69 = 0.
• B. 3x² – 90x + 168 = 0.
• C. 3x² – 90x + 375 = 0.
• D. 3x² – 90x – 207 = 0.
• E. x² – 30x – 125 = 0.

• A. – 2
• B. 3
• C. 3/2
• D.
• E. 6

A Secretaria de Estado da Cultura iria distribuir 19 500 livros igualmente entre x bibliotecas. No entanto, 6 dessas bibliotecas deixaram de receber, pois já haviam recebido livros da prefeitura. Desse modo, as que ganharam os livros da Secretaria de Estado da Cultura receberam 225 livros a mais do que receberiam, caso os livros fossem divididos entre todas as bibliotecas indicadas inicialmente.

• A.
• B.
• C.
• D.
• E.