Questões de Matemática

• A. 3.012
• B. 3.182
• C. 3.236
• D. 3.415
• E. 3.585

Atente às tabelas financeiras que encontram-se nas páginas 16 e 17.

• A.

  

• B.
• C.
• D.
• E.

Voando em um helicóptero, um fotógrafo consegue realizar um mapeamento fotográfico de forma a fotografar 3 km² a cada 17 minutos. Supondo-se que esse fotógrafo mantenha a mesma razão entre superfície mapeada e tempo gasto, o tempo necessário para mapear 20 km² será

• A. maior do que 1 hora e 15 minutos e menor do que 1 hora e 30 minutos.
• B. maior do que 1 hora e 30 minutos e menor do que 1 hora e 45 minutos.
• C. maior do que 2 horas.
• D. maior do que 1 hora e 45 minutos e menor do que 2 horas.
• E. menor do que 1 hora e 15 minutos.

A matriz quadrada A, definida genericamente por A = aij, é dada por a11 = 0; a12 = - 4; a13 = 2; a21 = x; a22 = 0; a23 = (1 - z); a31 = y; a32 = 2z e, por último, a33 = 0. Desse modo, para que a matriz A seja uma matriz antissimétrica, os valores de a21, a23, a31 e a32 deverão ser, respectivamente, iguais a:

• A. 4; -2; -2; -2.
• B. 4; -2; 2; -2.
• C. 4; 2; -2; -2.
• D. -4; -2; 2; -2.
• E. -4; -2; -2; -2.

Se existe um padrão para a obtenção dos elementos da sequência 1, 27, 125, x, 729, o valor de x é

• A. 343.
• B. 373.
• C. 515.
• D. 617.
• E. 618.

Três irmãos, Uguinho, Luizinho e Zezinho, ao confrontarem suas contas de telefone celular, ficaram curiosos em saber quanto custou um minuto de cada tipo de ligação realizada. As três contas apresentaram ligações para telefones fixos e móveis (celulares) e ligações internacionais para a Patagônia, onde moram seus primos. A tabela abaixo informa o tempo (em minutos) das ligações que cada um efetuou e o valor correspondente da conta, já descontado o preço da assinatura.

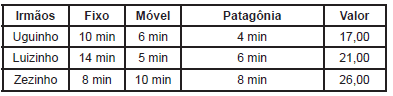
Vamos denominar x, y e z os preços do minuto de ligação para telefones fixos, para telefones móveis e para a Patagônia, respectivamente. x, y e z, respectivamente, custaram:

• A. R$ 1,50, R$ 2,00 e R$ 2,50.
• B. R$ 1,00, R$ 1,50 e R$ 2,00.
• C. R$ 0,50, R$ 1,00 e R$ 1,50.
• D. R$ 1,00, R$ 2,00 e R$ 2,50.
• E. R$ 0,50, R$ 2,00 e R$ 2,50.

A razão entre a medida do comprimento e a medida da largura de uma foto retangular é, nessa ordem, x. Ao serem duplicadas as medidas dos lados dessa foto retangular, a razão entre a medida do comprimento e a medida da largura é, nessa ordem, é igual a

• A. x/2.
• B. x.
• C. 4x.
• D. 2x.
• E. x/4.

Em um cofre estão guardados 5 anéis: dois de ouro e três de prata. Aleatoriamente, retiram-se dois anéis do cofre, um após o outro e sem reposição. Define-se a variável aleatória X igual a 1 se o primeiro anel retirado é de prata, e igual a 0 se este é de ouro. De modo análogo, definese a variável aleatória Y igual a 1 se o segundo anel é de prata, e 0 se este é de ouro. Desse modo, a covariância de X e Y ─ Cov(X,Y) ─ é igual a:

• A. 0
• B. 1
• C. -1
• D. 3/50
• E. -3/50

Dados os conjuntos A={}, B={{}} e C={{2},{3,4}}, é correto afirmar que

• A. as cardinalidades de A e B são iguais.
• B. as cardinalidades de A e C são iguais.
• C. as cardinalidades de B e C são iguais.
• D. suas cardinalidades são diferentes entre si.
• E. a cardinalidade de C é superior a de B em 2 elementos.

Sabendo-se que a trajetória de uma flecha lançada obliquamente, desprezados os efeitos do ar, é uma parábola. Uma flecha lançada a partir do solo descreve uma parábola de equação Y = 120X − 4X² (X e Y em metros).

Analisar as declarações a seguir:

I - A flecha começará a retornar ao solo no intervalo, 0 ≤ X ≤ 30.

II - As raízes da parábola permitem saber o alcance máximo atingido pela flecha.

III - A altura máxima atingida pela flecha será de 500 metros.

IV - A flecha atingirá o solo após ter percorrido a distância de 30 metros.

V - A flecha atingirá sua altura máxima quando percorrer a distância de 15 metros.

Das declarações acima, escolha a única alternativa correta.

• A. Estão corretos apenas os itens ímpares.
• B. Estão incorretos apenas os itens II e III.
• C. Está incorreto apenas o item III.
• D. Estão incorretos os itens I, IV e V.
• E. Estão corretos apenas os ítens III e IV.