Questões de Matemática do ano 0000

Numa frota de veículos, certo tipo de manutenção é feito no veículo A a cada 3 dias, no veículo B a cada 4 dias e no veículo C a cada 6 dias, inclusive aos sábados, domingos e feriados. Se no dia 2 de junho de 2003 foi feita a manutenção dos três veículos, a próxima vez em que a manutenção dos três ocorreu no mesmo dia foi em

• A. 05/06/03
• B. 06/06/03
• C. 08/06/03
• D. 14/06/03
• E. 16/06/03

Um auxiliar deve arquivar em pastas um certo número de documentos iguais. Se ele colocar 75 documentos em cada pasta, ele usará 50 pastas. Entretanto, se ele colocar 30 documentos em cada pasta, de quantas pastas precisará?

• A. 45
• B. 100
• C. 110
• D. 112
• E. 125

O gráfico abaixo representa o movimento de um projétil que foi lançado da origem (0,0), segundo uma trajetória parabólica, cuja função pode ser representada por y=ax2+bx, onde y representa a distância vertical atingida (altura), em metros e x representa a distância horizontal percorrida, a partir da origem, em metros.

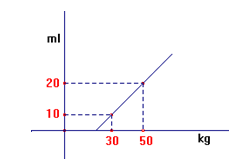
Sabendo-se que a altura máxima atingida é 3 metros e que o projétil vai atingir o solo a 2 metros de distância da origem, assinale a alternativa que apresenta os valores de a e b, nesta ordem

• A.

  -3 e 6

• B.

  3 e -6

• C.

  -6 e 3

• D.

  6 e -3

A função g: R ->R (veja gráfico), é tal que g(x) = 6 para todo x 10 e g(x) = 1, para todo x 0.

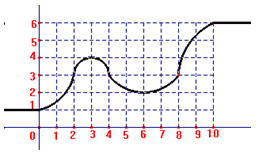
Sobre a equação g(x) = 3 é correto afirmar:

• A.

  possui exatamente três raízes reais

• B.

  possui exatamente duas raízes reais

• C.

  possui exatamente uma raiz real

• D.

  não possui raízes reais

A reta do gráfico abaixo representa a quantidade total de medicamento (em ml) que uma pessoa pode tomar, em função do seu peso/massa (em kg).

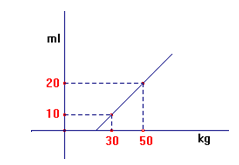
Assim, uma pessoa de 30 kg pode tomar um total de 10 ml do medicamento, enquanto uma pessoa de 50 kg pode tomar um total de 20 ml. Para um paciente de 90 kg, foi receitado esse medicamento, sendo que o total que ele pode tomar deve ser dividido em 5 doses iguais. Assinale a alternativa que apresenta o número de ml do medicamento que o paciente deve tomar, em cada dose.

• A.

  6 ml

• B.

  8 ml

• C.

  10 ml

• D.

  12 ml

Seja X = a - 3ab +2a²c. Assinale a alternativa que apresenta os valores de b e c, nesta ordem, sabendo que: para a=-1, o valor de X é 2 e para a=2, o valor de X é 32

• A.

  3 e –1

• B.

  1 e –3

• C.

  -1 e 3

• D.

  –3 e 1

• A.

  1° quadrante

• B.

  2º quadrante

• C.

  3º quadrante

• D.

  4º quadrante

Se A, B e C são três grandezas, em que A é diretamente proporcional a B e inversamente proporcional ao quadrado de C, então a expressão algébrica que melhor representa essas relações é:

• A.

  A=B/C.

• B.

  B=A/C.

• C.

  A=B/C2.

• D.

  A=BC2.

• E.

  A=BC.

Se A e B são raízes da equação 3x²- 4x+1=0, então o valor absoluto da diferença entre A e B é

• A.

  1/3.

• B.

  2/3

• C.

  4/3.

• D.

  5/3.

• E.

  2.

Uma das condições para que o servidor público do sexo masculino adquira o direito à aposentadoria é que sua idade mais o tempo de contribuição à previdência seja igual a 95 anos, com tempo mínimo de contribuição de 35 anos. Nessas condições, a idade que o servidor deverá começar a contribuir para adquirir o direito à aposentadoria com o tempo mínimo de contribuição é

• A.

  16 anos.

• B.

  18 anos.

• C.

  20 anos

• D.

  25 anos.

• E.

  28 anos.