Questões de Matemática do ano 2003

Com três segmentos de comprimentos iguais a 10 cm, 12 cm e 23 cm:

• A.

  É possível formar apenas um triângulo acutângulo.

• B.

  É possível formar apenas um triângulo obtusângulo.

• C.

  É possível formar apenas um triângulo retângulo.

• D.

  Não é possível formar um triângulo.

Na Matemática, o conceito de função é freqüentemente utilizado para a modelagem de situações-problema reais. Com respeito a funções tradicionais e bem conhecidas, julgue os itens subseqüentes.

Sabendo que tg =  , então a altura do muro representado na figura abaixo é igual a 3 m.

• C. Certo
• E. Errado

Um retângulo tem 21 cm de perímetro e 20 cm² de área. Quanto medem seus lados?

• A. 8 cm e 2,5 cm.
• B. 2 cm e 10 cm.
• C. 4 cm e 5 cm.
• D. 3 cm e 7 cm.

Um volume de 1200 ml de água foi distribuído igualmente em certo número de copos. Depois, de novo com 1200 ml de água, fez-se a mesma coisa, mas foram colocados 50 ml de água a menos por copo, e por isso foram necessários mais 2 copos. Em quantos copos a água foi distribuída da primeira vez?

• A.

  7 copos.

• B.

  6 copos.

• C.

  8 copos.

• D.

  10 copos.

O número 310 está dividido em três parcelas de tal maneira que a segunda parcela é igual a 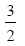 da primeira e a terceira é igual a  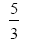da segunda. Qual é o valor da menor das parcelas?

• A. 65
• B. 65
• C. 54
• D. 48

Na revista da Associação Brasileira das Empresas de Transporte Rodoviário Intermunicipal, Interestadual e Internacional de Passageiros (ABRATI), de março de 2002, foi publicada a tabela abaixo, que traz o número de mortes ocorridas na Rodovia Presidente Dutra, que liga a cidade do Rio de Janeiro à capital paulista, entre os anos de 1997 e 2000.

De acordo com um conhecido método da Matemática, denominado Método dos Quadrados Mínimos (MQM), esses valores podem ser ajustados (modelados) por uma função linear da forma f(t) = at + b. O ajuste da função, com os dados fornecidos na tabela, está esboçado no gráfico a seguir.

Para se conhecer os números reais a e b que definirão a função linear f(t) será necessário resolver o seguinte sistema de equações lineares, segundo o MQM:

Com base nessas informações, julgue os itens que se seguem.

Considerando a = -67 e b = 437, conclui-se que o número de mortes no ano 2002 deve ter sido menor que 120.

• C. Certo
• E. Errado

Na revista da Associação Brasileira das Empresas de Transporte Rodoviário Intermunicipal, Interestadual e Internacional de Passageiros (ABRATI), de março de 2002, foi publicada a tabela abaixo, que traz o número de mortes ocorridas na Rodovia Presidente Dutra, que liga a cidade do Rio de Janeiro à capital paulista, entre os anos de 1997 e 2000.

De acordo com um conhecido método da Matemática, denominado Método dos Quadrados Mínimos (MQM), esses valores podem ser ajustados (modelados) por uma função linear da forma f(t) = at + b. O ajuste da função, com os dados fornecidos na tabela, está esboçado no gráfico a seguir.

Para se conhecer os números reais a e b que definirão a função linear f(t) será necessário resolver o seguinte sistema de equações lineares, segundo o MQM:

Com base nessas informações, julgue os itens que se seguem.

Resolvendo o sistema (I), obtém-se para b um valor menor que 437.

• C. Certo
• E. Errado

Em cada um dos itens seguintes, é apresentada uma situação hipotética, seguida de uma assertiva a ser julgada.

A soma e o produto das quantidades de horas trabalhadas por um empregado em dois dias consecutivos são, respectivamente, iguais a 14 e 48. Ele trabalhou mais no primeiro dia que no segundo. Nessa situação, o número de horas trabalhadas no segundo dia é igual a  do número de horas trabalhadas no primeiro dia.

• C. Certo
• E. Errado

Usando dois tipos de bronze, um com 62% e o outro com 70% de cobre, pretende-se obter uma tonelada de um novo tipo de bronze com exatamente 65% de cobre. Para isto deve-se usar:

• A.

  700 quilos do primeiro tipo e 300 quilos do segundo

• B.

  725 quilos do primeiro tipo e 275 quilos do segundo

• C.

  625 quilos do primeiro tipo e 375 quilos do segundo

• D.

  650 quilos do primeiro tipo e 350 quilos do segundo

• E.

  800 quilos do primeiro tipo e 200 quilos do segundo

Se um produtor de café misturar 2 kg de café em pó do tipo I com 3 kg de café do tipo II ele obtém uma mistura cujo preço é de R$ 4,80 o quilograma. Ao misturar 3 kg de café em pó do tipo I com 2 kg de café do tipo II, a nova mistura custará R$ 5,20 o quilograma. O preço do quilograma de café do tipo I e do tipo II são respectivamente:

• A. R$ 1,20 e R$ 0,80
• B. R$ 0,80 e R$ 1,20
• C. R$ 6,40 e R$ 4,00
• D. R$ 7,00 e R$ 4,00
• E. R$ 6,00 e R$ 4,00