Questões de Matemática do ano 2007

O nivelamento trigonométrico corresponde a um método utilizado em topografia e geodésia para obter cotas e(ou) altitudes por meio de medições de ângulos verticais e distâncias horizontais. Com referência a essas informações e considerando a ilustração acima, julgue os itens a seguir.

Na figura, o comprimento h i corresponde à altura do teodolito.

• C. Certo
• E. Errado

Uma escada com 10 m de comprimento foi apoiada em uma parede perpendicular ao solo de tal modo que o pé da escada ficou afastado 6 m da base da parede. Qual é a altura alcançada pela escada?

• A.

  9 m

• B.

  10 m

• C.

  16 m

• D.

  14 m

• E.

  8 m

• A.

• B.

• C.

• D.

• E.

Na figura, as retas PA e PC são tangentes à circunferência, e o ângulo APC mede 50º. As medidas dos ângulos ABC e ADC são, respectivamente,

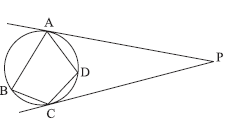
• A.

  90º e 90º.

• B.

  80º e 100º.

• C.

  75º e 105º.

• D.

  70º e 110º.

• E.

  65º e 115º.

Um observador em uma planície vê ao longe uma torre de transmissão segundo um ângulo de 30º (vide figura).

Após caminhar uma distância de 40 m em direção à torre, ele passa a vê-la segundo um ângulo de 45º. A altura da torre é, aproximadamente, de

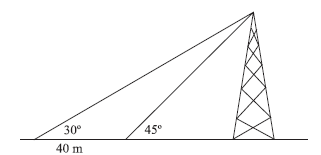
• A.

  45 m.

• B.

  55 m.

• C.

  64 m.

• D.

  80 m.

• E.

  94 m.

Quando um raio de luz é refletido em uma superfície lisa, o ângulo formado pelo raio incidente com a superfície é congruente ao ângulo formado pelo raio refletido com a superfície. Na figura, os ângulos ABC e BCD medem, respectivamente, 90º e 70º e o raio incidente faz um ângulo de medida x = 30º com a superfície AB. Sob que ângulo o raio incide em AB na segunda vez?

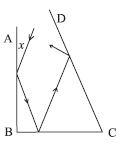
• A.

  40º.

• B.

  50º.

• C.

  60º.

• D.

  70º.

• E.

  80º.

Num triângulo equilátero, de área 3 cm² inscreve-se outro triângulo eqüilátero, de modo que cada lado do novo triângulo é perpendicular a um lado do triângulo inicial. A área da região exterior ao menor triângulo, mas interior ao maior, é:

• A.

  2 cm²

• B.

  ¡î3 cm©÷

• C.

  1,5 cm²

• D.
• E.

  1 cm2

Copérnico, em seu trabalho intitulado De Revolutionibus, propõe o problema a seguir.

"Dados os três lados de um triângulo isósceles, achar os ângulos da base".

 Para resolver o problema, ele utiliza a seguinte figura.

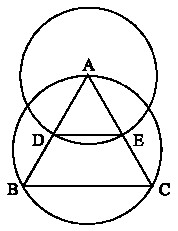
 A partir dessas informações e considerando que o triângulo ABC ilustrado acima é isósceles com base BC e que AD = AE =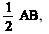

julgue os itens abaixo.

 I O ângulo 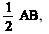 é igual à metade do ângulo  .

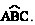II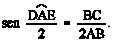 

III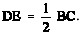  

 IV O centro do círculo que passa pelos pontos A, B e C é o ponto médio do segmento DE.

Estão certos apenas os itens

• A.

  I e II.

• B.

  I e IV.

• C.

  II e III.

• D.

  III e IV.

O Brasil foi descoberto no século XV pelos portugueses, época em que os europeus estavam explorando o resto do mundo. Métodos matemáticos para resolver problemas de navegação eram importantes nessa época. O país que empregasse novas técnicas tinha mais vantagem na conquista de novas colônias e de suas riquezas naturais. Entre os matemáticos da época, estão Regiomontanus e Copérnico.

Desde a antiguidade, o conhecimento da trigonometria e de relações métricas em um triângulo permite resolver problemas relacionados ao cálculo de distâncias inacessíveis. No livro II do trabalho intitulado Sobre Triângulos, Regiomontanus resolveu uma situação análoga à apresentada a seguir.

"Achar os lados AB e AG do triângulo ABG acutângulo mostrado a seguir, sabendo-se que BG = 8, a perpendicular AD = 3 e  "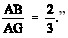

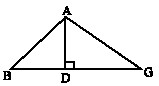
Para isso, ele escolheu um ponto E pertencente a DG tal que DE = BD, considerou que EG = 2x e reduziu o problema à determinação do valor de x.

 Considerando a situação apresentada no texto, assinale a opção correta acerca de x e do triângulo ABG.

• A.

  

• B.

  

• C.

  

• D.

  

Utilizando construções geométricas, com régua e compasso, um aluno transformou um quadrilátero ABCD em um triângulo PCD, ambos com interior de mesma área. Veja como foi seu procedimento.

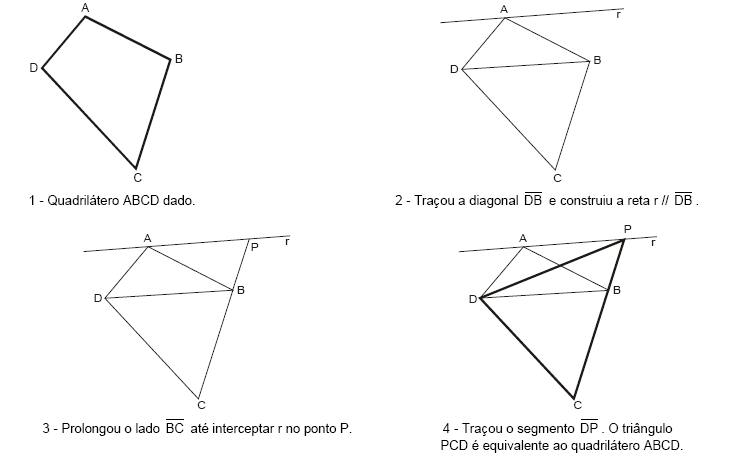
Essa construção de triângulo equivalente a um quadrilátero está baseada no fato de que

• A.

  os triângulos PDB e DBC têm a mesma área, pois têm um lado comum.

• B.

  a soma das áreas dos triângulos ADB e PDB é igual à área do triângulo DBC.

• C.

  os triângulos PDB e BDC são semelhantes.

• D.

  os triângulos ADB e PDB têm a mesma área, pois têm a mesma altura.

• E.

  o quadrilátero ABCD tem o mesmo perímetro que o triângulo PDC.