Questões de Matemática do ano 2010

A 19a Copa do Mundo de Futebol foi disputada na África do Sul, do dia 11 de junho ao dia 11 de julho de 2010. Em todas as edições da Copa, durante a 1ª fase da competição, cada seleção joga somente contra as equipes do grupo que integra, uma única vez apenas contra cada uma delas.

Na África do Sul, as 32 seleções participantes foram divididas em 8 grupos de 4 equipes. Portanto, cada equipe jogou uma única vez contra cada uma das outras 3 equipes de seu grupo. Assim, ao final da 1ª fase, foram realizados, ao todo, 48 jogos.

Se a competição vier a ser disputada por 35 seleções divididas em 7 grupos de 5 equipes, ao final da 1ª fase, o número total de jogos realizados será de

• A.

  35

• B.

  70

• C.

  92

• D.

  105

• E.

  140

Apesar de ser um dos mais famosos matemáticos Bhaskara, que viveu no séc. XII, não contribuiu diretamente na elaboração da fórmula que leva seu nome. Na história da Matemática podemos encontrar egípcios, babilônios, gregos, outros hindus e chineses. Entre eles podemos destacar, Euclides, Diophanto, Al-Khowârizmî, Zhu Shijie (também chamado Chu Shih-Chieh).

No século XIX o método foi redescoberto por Willian George Horner e Theophilus Holdred e, um pouco antes por Paolo Ruffini. O que ficou conhecido como método de Horner, já tinha sido antecipado por Isaac Newton em 1669. No século XVI, François Viéte utilizou-se de simbolismo para representar esse processo.

A contribuição atribuída a Bhaskara serve para

• A.

  determinar quais são os números primos compreendidos entre 1 e 100.

• B.

  determinar medidas proporcionais em figuras semelhantes.

• C.

  relacionar as medidas dos catetos com a hipotenusa de um triângulo retângulo.

• D.

  a resolução de uma equação de 2o grau.

• E.

  determinar o máximo divisor comum entre dois ou mais números.

A professora de uma sala de aula de 8o ano resolveu fazer um levantamento das alturas de seus 35 alunos para compará-las com sua média aritmética. Percebeu que todos os números encontrados pertencem ao conjunto dos números

• A.

  inteiros, mas não ao conjunto dos números naturais.

• B.

  racionais não negativos.

• C.

  reais não positivos.

• D.

  racionais não positivos.

• E.

  complexos, mas não ao conjunto dos números reais.

Ao discutir um conteúdo matemático com seus alunos, o professor propôs o seguinte problema:

Ana e Bruno, juntos, têm mais do que 3 litros de tinta branca. A diferença entre o triplo da quantidade de tinta de Bruno e o dobro da quantidade de tinta de Ana, nessa ordem, é maior que meio litro. Apresente uma representação geométrica das soluções dos pares ordenados (A,B) que indiquem todas as possibilidades da quantidade A de tinta branca de Ana, em litros, e da quantidade B de tinta branca de Bruno, em litros.

Para que a questão proposta possa ser resolvida com máximo rigor matemático, os alunos terão que trabalhar com

• A.

  potências e árvore de possibilidades.

• B.

  equação geral da circunferência e de elipse.

• C.

  sistema de equações e representação dos pares (A,B) em tabelas.

• D.

  sistema de inequações e sua representação no plano cartesiano.

• E.

  conservações de unidades de medidas e gráfico de setores.

Sabe-se que, no instante em que a água de um poço ocupava 2/5 de sua capacidade, alguns operários foram designados para a operação de retirada da água de seu interior e, que, para tal, usaram apenas recipientes com capacidade igual a 7/4 de litro. Se o poço tinha capacidade para C litros d'água e 41 930 < C < 42 000, o número mínimo de vezes que esses recipientes foram usados até que o poço ficasse completamente vazio é igual a

• A.

  8 750.

• B.

  8 995.

• C.

  9 180.

• D.

  9 375.

• E.

  9 590.

Suponha que, na fabricação de n unidades de certo produto, são previstos, em reais, um custo C(n) = 3n + 20 e um lucro L(n) = 8n – 30. Para que o lucro supere 250% do custo, o número mínimo de unidades desse produto que devem ser vendidas é igual a

• A.

  11.

• B.

  50.

• C.

  143.

• D.

  161.

• E.

  175.

Chama-se fração decimal toda fração da forma 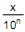 , em que 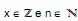. Com base nessa definição, se 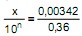, é correto concluir que:

• A.

  x < 100 e n > 5

• B.

  50 < x < 80 e n < 5

• C.

  x + n = 100

• D.

  x é ímpar e n é par

• E.

  x e n são ímpares

Os termos da sequência (12, 15, 9, 18, 21, 15, 30, 33, 27, 54, 57, . . .) são sucessivamente obtidos através de uma lei de formação. Se x e y são, respectivamente, o décimo terceiro e o décimo quarto termos dessa sequência, então:

• A.

  x . y = 1530

• B.

  y = x + 3

• C.

  x = y + 3

• D.

  y = 2x

• E.

  x/y = 33/34

Seja ∆ a operação definida por u^∆ = 3 − 5u, qualquer que seja o inteiro u. Calculando (-2)^∆ + (2^∆)^∆  obtém-se um número compreendido entre:

• A.

  −20 e −10

• B.

  −10 e 20

• C.

  20 e 50

• D.

  50 e 70

• E.

  70 e 100

Em uma prova com X questões a nota máxima é 10,0 e odas elas têm o mesmo valor. Suponha que um aluno acerte 18 das 32 primeiras questões e, das restantes, ele acerte 40%. Assim sendo, se esse aluno tirou nota 5,0 nessa prova, então X é um número

• A.

  múltiplo de 4.

• B.

  divisível por 17.

• C.

  menor que 50.

• D.

  primo.

• E.

  quadrado perfeito.