Questões de Matemática do ano 2012

Sabe-se que 1 é uma das raízes da equação x³ - – 2x² + 3x – 2 = 0. Pode-se afirmar, dessa forma, que as demais raízes são

• A.

  racionais e iguais.

• B.

  racionais e diferentes.

• C.

  irracionais e iguais.

• D.

  irracionais e diferentes.

• E.

  complexas.

• A.

  apenas I.

• B.

  apenas I e II.

• C.

  apenas I, II e III.

• D.

  apenas I, II, III e IV.

• E.

  I, II, III, IV e V.

• A.

  -12

• B.

  -4

• C.

  -1

• D.

  2

Considere a igualdade x + (4 + y) . i = (6 − x) + 2yi , em que x e y são números reais e i é a unidade imaginária. O módulo do número complexo z = x + yi, é um número

• A.

  maior que 10.

• B.

  quadrado perfeito.

• C.

  irracional.

• D.

  racional não inteiro.

• E.

  primo.

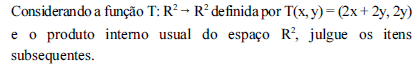
ara quaisquer números reais x e y, o vetor T(x, y) tem o dobro do comprimento do vetor (x, y).

• C. Certo
• E. Errado

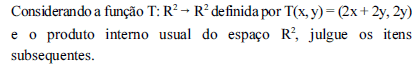
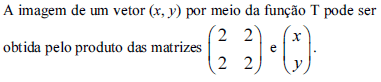
• C. Certo
• E. Errado

Um consumidor dispõe de R$ 600,00 para gastar em dois produtos. A unidade do primeiro produto custa R$ 20,00 e a do segundo R$ 30,00. A satisfação do consumidor ao adquirir x unidades do primeiro produto e y unidades do segundo é medida pela função U(x,y) = 10x3/5y2/5. Com base nessas informações, julgue os itens a seguir.

O campo vetorial gerado pelo gradiente da função determinada pela restrição orçamentária do consumidor é constante.

• C. Certo
• E. Errado

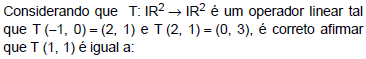
• A.

  (4, −1)

• B.

  (4, 1)

• C.

  (2, 4)

• D.

  (2, −2)

• E.

  (0, 5)

É correto afirmar que

• A.

  a dimensão de V é igual a 1.

• B.

  o conjunto {(1, 1, 2)} é uma base de V.

• C.

  a dimensão de V é igual a 2.

• D.

  o conjunto {(1, −1, 0), (− 1, 0, 2)} é uma base de V.

• E.

  a dimensão de V é igual a 3.

NÃO é um conjunto gerador de U:

• A.

  {(1, 1, 0), (1, 0, −1)}

• B.

  {(−2, 0, 2), (1, −1, −2)}

• C.

  {(1, 2, 1), (−1, 0, 1)}

• D.

  {(3, 2, −1), (2, 4, 2)}

• E.

  {(1, −2, 1), (1, 0, 1)}