Questões sobre Cálculo Aritmético

Iniciando seu treinamento, dois ciclistas partem simultaneamente de um mesmo ponto de uma pista. Mantendo velocidades constantes, Lucas demora 18 minutos para completar cada volta, enquanto Daniel completa cada volta em 15 minutos. Sabe-se que às 9 h 10 min eles passaram juntos pelo ponto de partida pela primeira vez, desde o início do treinamento. Desse modo, é correto afirmar que às 8 h 25 min, Daniel já havia completado um número de voltas igual a

• A. 2.
• B. 3.
• C. 4.
• D. 5.
• E. 7.

Sabe-se que, na usinagem das faces de uma peça, será utilizada uma fresa H com 10 dentes e 40mm de diâmetro. Sabendo que a velocidade de corte será igual a 21m/min, e admitindo, ainda, que π = 3, a rotação da fresa, em rpm, vale, aproximadamente:

• A. 125
• B. 150
• C. 175
• D. 200
• E. 225

Uma cooperativa faz sabão com óleo de cozinha reciclado. Depois de filtrado, aquecido e filtrado novamente, o óleo usado recebe soda cáustica e outras substâncias e é despejado em grandes formas. Solidificada, a massa é cortada em pedaços iguais, que são embalados em caixas. Se o número total de pedaços obtidos em certo lote, que está compreendido entre 1 400 e 1 600 unidades, for repartido em caixas contendo, cada uma, 20 unidades, ou 36 unidades, ou 40 unidades, ou 48 unidades, sobrarão sempre 8 pedaços. Desse modo, é correto afirmar que o produto dos algarismos do número de pedaços obtidos nesse lote foi igual a

• A. zero.
• B. 24.
• C. 64.
• D. 96.
• E. 128.

Em certa ocasião, 20 funcionários necessitaram de 24 horas de trabalho para catalogar 400 objetos. Outros 400 objetos, de mesmo tipo dos 400 primeiros, precisam ser catalogados e o responsável quer que sejam catalogados em 10 horas de trabalho. Para isso acontecer, é necessário atribuir essa tarefa para um número de funcionários, com a mesma capacidade dos já citados, igual

• A. 80.
• B. 64.
• C. 48.
• D. 60.
• E. 30.

Sabe-se que 15 funcionários conseguem arquivar 450 processos por dia. Vinte e cinco funcionários, com a mesma capacidade dos anteriores, arquivariam por dia uma quantidade de processos igual a

• A. 450.
• B. 750.
• C. 425.
• D. 585.
• E. 675.

Uma verba de R$ 65.000,00 será alocada a três projetos diferentes. A divisão desse dinheiro será realizada de forma diretamente proporcional aos graus de importância dos projetos, que são, respectivamente, 2, 4 e 7. Dessa maneira, a quantia que o projeto mais importante receberá ultrapassa a metade do total da verba em

• A. R$ 2.500,00.
• B. R$ 9.000,00.
• C. R$ 1.000,00.
• D. R$ 5.000,00.
• E. R$ 7.500,00.

Três irmãos, Uguinho, Luizinho e Zezinho, ao confrontarem suas contas de telefone celular, ficaram curiosos em saber quanto custou um minuto de cada tipo de ligação realizada. As três contas apresentaram ligações para telefones fixos e móveis (celulares) e ligações internacionais para a Patagônia, onde moram seus primos. A tabela abaixo informa o tempo (em minutos) das ligações que cada um efetuou e o valor correspondente da conta, já descontado o preço da assinatura.

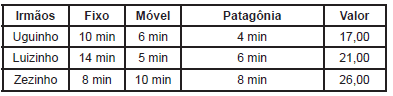
Vamos denominar x, y e z os preços do minuto de ligação para telefones fixos, para telefones móveis e para a Patagônia, respectivamente. x, y e z, respectivamente, custaram:

• A. R$ 1,50, R$ 2,00 e R$ 2,50.
• B. R$ 1,00, R$ 1,50 e R$ 2,00.
• C. R$ 0,50, R$ 1,00 e R$ 1,50.
• D. R$ 1,00, R$ 2,00 e R$ 2,50.
• E. R$ 0,50, R$ 2,00 e R$ 2,50.

Sobre um plano horizontal e iluminadas lateralmente pela luz solar direta, estão colocadas uma haste vertical com 10 cm de altura e uma pirâmide reta com 15 cm de altura, cuja base é um quadrado com 10 cm de lado. Sabendo-se que a haste projeta uma sombra de 12 cm sobre esse plano, a pirâmide projetará uma sombra cujo comprimento, medido em relação ao centro de sua base, será de

• A. 15 cm.
• B. 8 cm.
• C. 23 cm.
• D. 18 cm.
• E. 13 cm.

Um jogo de vôlei entre duas equipes é ganho por aquela que primeiro vencer três sets, podendo o placar terminar em 3 a 0, 3 a 1 ou 3 a 2. Cada set é ganho pela equipe que atingir 25 pontos, com uma diferença mínima de dois pontos a seu favor. Em caso de igualdade 24 a 24, o jogo continua até haver uma diferença de dois pontos (26 a 24, 27 a 25, e assim por diante). Em caso de igualdade de sets 2 a 2, o quinto e decisivo set é jogado até os 15 pontos, também devendo haver uma diferença mínima de dois pontos. Dessa forma, uma equipe pode perder um jogo de vôlei mesmo fazendo mais pontos do que a equipe adversária, considerando-se a soma dos pontos de todos os sets da partida. O número total de pontos da equipe derrotada pode superar o da equipe vencedora, em até

• A. 44 pontos.
• B. 50 pontos.
• C. 19 pontos.
• D. 25 pontos.
• E. 47 pontos.

Amanda utiliza pequenas caixas retangulares, de dimensões 20 cm por 20 cm por 4 cm, para embalar as trufas de chocolate que fabrica em sua casa. As trufas são redondas, tendo a forma de bolas (esferas) de 4 cm de diâmetro. Considerando que as caixas devem ser tampadas, a máxima quantidade de trufas que pode ser colocada em uma caixa desse tipo é igual a

• A. 32.
• B. 25.
• C. 20.
• D. 16.
• E. 12.