Questões sobre Equaçõess trigonométricas

Os ângulos internos de um triângulo medem 90°, 60° e 30°. Se o maior lado desse triângulo mede 10cm, o menor mede:

• A.

  3cm

• B.

  

• C.

  5cm

• D.

  

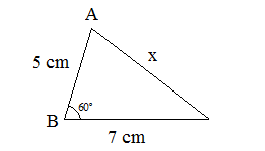
Calcule o valor de x no triângulo escaleno abaixo.

• A.

  

• B.

  

• C.

  

• D.

  

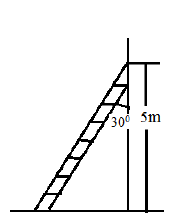
Um pedreiro apoia uma escada na parede, conforme a figura abaixo. A escada se apoia na parede 5 metros de distância do solo e forma com esta parede, neste local, um ângulo de 30º. Qual o comprimento da escada em metros, aproximadamente? Considere: sen 30º= 0,5 e cos 30º= 0,87.

• A.

  4,35m;

• B.

  2,5m;

• C.

  5,74m;

• D.

  10m.

Observe a figura abaixo.

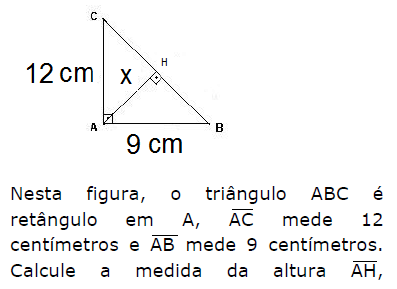
representada na figura por X, e marque a opção correta.

• A.

  5 cm;

• B.

  7,2 cm;

• C.

  15 cm;

• D.

  18,6 cm.

Dado que cotg X = 1 e sendo X um ângulo do terceiro quadrante, 2 então 5 sen X, é igual a?

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

Seja 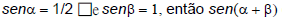 é igual a:

• A.

  1/4

• B.

  

• C.

  

• D.

Sendo 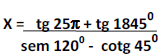 então podemos afirmar que X, é igual a?

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

• A.

  reflexão na origem.

• B.

  reflexão em torno do eixo x.

• C.

  rotação no sentido anti-horário em torno da origem.

• D.

  rotação no sentido horário em torno da origem.

• E.

  translação em torno da origem.

O desenho acima é um esquema simplificado de uma bomba de sucção de petróleo. O motor faz a roda girar, o que movimenta o braço de ligação entre a roda e o corpo da bomba. O braço está conectado à roda no ponto p. Nessa situação, considere que o movimento do ponto p ao longo da roda seja descrito pela função , em que x represente o tempo, em minutos, e que F(0) = 0 signifique que os pontos p e q da figura estejam alinhados com o centro C da roda, ou seja, sobre uma mesma reta horizontal, à menor distância possível entre eles, e o corpo da bomba também esteja na posição horizontal. Considere, além disso, que o movimento da roda seja no sentido horário. Com base nessas informações, julgue os itens seguintes.

Se, em determinado instante durante o movimento da roda, a cabeça da bomba estiver na posição mais próxima do solo, decorrerão, no máximo, mais 10 minutos até que a cabeça da bomba esteja novamente nessa mesma posição.

• C. Certo
• E. Errado