Questões sobre Geometria Plana

Leia o texto 'Teorema de Pitágoras' e, em seguida, analise as afirmativas abaixo:

I. Segundo o texto, o teorema de Pitágoras também pode ser enunciado como uma relação entre áreas, pois, em qualquer triângulo retângulo, a área do quadrado cujo lado é a hipotenusa é igual à soma das áreas dos quadrados cujos lados são os catetos, de acordo com o texto.

II. É verdadeira a equação: c² = b² + a², onde “a” representa o comprimento da hipotenusa, e “b” e “c” representam os comprimentos dos outros dois lados do triângulo, de acordo com o texto.

III. O 5º passo para a demonstração do teorema de Pitágoras utilizando a comparação de áreas, de acordo com as informações do texto, é desenhar o quadrado de lado b + a, colocando-se os quatro triângulos retângulos noutra posição dentro do quadrado: a posição que deixa desocupada uma região que é um quadrado de lado c, de acordo com o texto.

Marque a alternativa CORRETA:

Observe as dimensões do triângulo retângulo abaixo:

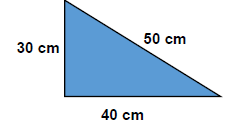
Qual a área desse triângulo retângulo?

A seguinte tabela apresenta a distância aproximada, em linha reta, entre a cidade de Itabaiana e quatro outras cidades de Sergipe.
Lagarto Aracaju Estância Poço Verde
Itabaiana 35 km 50 km 60 km 80 km
Com base nessas informações, é correto afirmar que um círculo com área de 3.200 km² centrado em Itabaiana

Ritinha deseja uma mesa diferente para a sua varanda, então solicitou ao marceneiro que fizesse a mesa no formato de um trapézio, com as seguintes medidas:
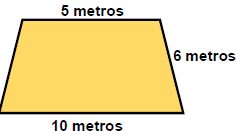Com os dados acima, qual será a área da mesa que Ritinha solicitou ao marceneiro?

João e Maria desejam montar uma linda horta no quintal, como os dois são professores de matemática, decidiram fazer os canteiros com formatos geométricos. Para o repolho o canteiro terá a forma de um círculo e para o canteiro de cenoura será no formato do triângulo escaleno. Como será esse canteiro de cenoura?

Se dois lados de um triângulo medem, respectivamente, 8cm e 10cm, pode-se afirmar que a medida do terceiro lado é

A malha quadriculada a seguir representa as quadras de um loteamento recém-construído. Os pontos A, B, M, N, P e Q são as posições das únicas 6 casas já prontas para serem ocupadas por moradores.

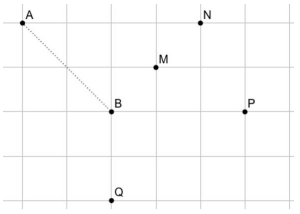
Um engenheiro fará uma inspeção nas casas, na ordem: ABMNPQ. Para isso, ele só pode se deslocar pelas linhas verticais e horizontais da malha, que representam as ruas do loteamento. Como referência, a distância entre as casas A e B, em linha reta (pontilhada), é de m.

Qual será a distância mínima a ser percorrida pelo engenheiro nessa rota?

Esperança Nova é um distrito que tem área de 5 km² . Se Esperança Nova tivesse a forma de um quadrado, então a medida de seus lados estaria entre

Analise as afirmativas a seguir:

I. Considere um triângulo com medidas iguais a 57 metros de base e 72 metros de altura. A partir desses dados, é correto afirmar que a área dessa figura geométrica é maior que 1.984 m².

II. Uma empresa precisa distribuir 3 camisas brancas para cada um dos seus 237 funcionários. Assim, considerando apenas os dados apresentados, é correto afirmar que essa empresa precisará de mais de 718 camisas e menos de 731 camisas para cumprir com a sua meta.

Marque a alternativa CORRETA:

Analise as afirmativas a seguir:

I. Um círculo com raio igual a 234 metros terá um perímetro menor que 1.512,12 metros.

II. Considerando uma gorjeta de 5% que foi paga pelo cliente, o valor final da conta de um restaurante foi igual a R$ 609. Assim, diante dos dados apresentados, é correto afirmar que o valor referente aos alimentos efetivamente consumidos, sem a gorjeta, era superior a R$ 578,33.

Marque a alternativa CORRETA: