Questões sobre Geometria Plana
Lista completa de Questões sobre Geometria Plana para resolução totalmente grátis. Selecione os assuntos no filtro de questões e comece a resolver exercícios.
Encontre o valor aproximado do seno do ângulo ? do triângulo abaixo.
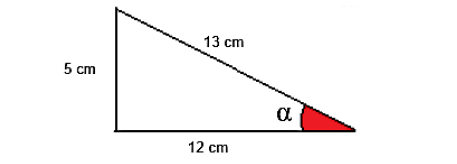
-
A) 0,38.
B) 0,92.
C) 0,41.
D) 1,24.
Escreva a equação geral da circunferência, que tem centro C (-2, 1) e raio r = ?5.
-
A) x² + y² + 4x - 2y =0.
B) x² + y² - 4x + 2y - 1 =0.
C) x² - y² + 5x - y =0.
D) x² - y² - 4x + y -2 =0.
E) 2x² - y² + 4x - y -5 =0.
O Pentágono é a sede do Departamento de Defesa dos Estados Unidos, sendo um símbolo das Forças Armadas dos EUA, o Pentágono é frequentemente utilizado metonimicamente para se referir ao Departamento de Defesa. Qual dos polímeros tem o formato do pentágono?
-
A)

B)

C)

D)

Determine o perímetro de um triangulo retângulo cujo cateto adjacente mede 12 cm e seu cosseno é igual a 0,8.
-
A) 36.
B) 48.
C) 60.
D) 72.
E) 90.
A administração municipal deseja construir a seguinte praça:

Usando o valor para ? = 3,14 , a área da praça será?
-
A) 113,04 m2 .
B) 1.340,36 m2 .
C) 1.017,36 m2 .
D) 2.025,46 m2 .
Uma praça está inscrita em uma área retangular cujos lados medem 300 m e 500 m, conforme a figura abaixo. Calculando a área da praça, quanto obtemos? Note que a praça é referente à área sombreada.
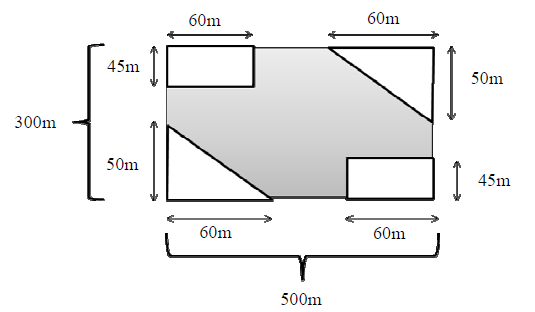

-
A) 138.600 cm²
B) 141.600 cm²
C) 147.000 cm².
D) 128.300 cm²
E) 148.600 cm².
Na composição de custos de um serviço de pintura de parede orçado por metro quadrado, o coeficiente do pintor é 1,5 hora, e o do ajudante é de 3,0 horas. A empresa costuma trabalhar com uma equipe formada por 1 pintor e 2 ajudantes.
Com base na situação hipotética precedente, é correto afirmar que o tempo esperado para que a equipe da empresa execute e conclua a pintura de 1 m2 de parede é de
Com base na situação hipotética precedente, é correto afirmar que o tempo esperado para que a equipe da empresa execute e conclua a pintura de 1 m2 de parede é de
-
A) 3 horas.
B) 4,5 horas.
C) 2,25 horas.
D) 1,5 hora.
E) 9 horas.
Teorema de Pitágoras
O teorema de Pitágoras é uma relação matemática entre os comprimentos dos lados de qualquer triângulo retângulo. Na geometria euclidiana, o teorema afirma que em qualquer triângulo retângulo, o quadrado do comprimento da hipotenusa é igual à soma dos quadrados dos comprimentos dos catetos.
Por definição, a hipotenusa é o lado oposto ao ângulo reto, e os catetos são os dois lados que o formam. Assim, o teorema de Pitágoras também pode ser enunciado como uma relação entre áreas: em qualquer triângulo retângulo, a área do quadrado cujo lado é a hipotenusa é igual à soma das áreas dos quadrados cujos lados são os catetos.
Para ambos os enunciados anteriormente mencionados, pode-se equacionar: c² = b² + a², onde c representa o comprimento da hipotenusa, e a e b representam os comprimentos dos outros dois lados.
A demonstração do teorema de Pitágoras utilizando a comparação de áreas pode ser feita da seguinte forma:
1. Desenha-se um quadrado de lado b + a;
2. Subdivide-se este quadrado em quatro retângulos, sendo dois deles quadrados de lados, respectivamente, a e b: Traça-se dois segmentos de reta paralelos a dois lados consecutivos do quadrado, sendo cada um deles interno ao quadrado e com o mesmo comprimento que o lado do quadrado;
3. Divide-se cada um destes dois retângulos em dois triângulos retângulos, traçando-se as diagonais. Chama-se c o comprimento de cada diagonal;
4. A área da região que resta ao retirar-se os quatro triângulos retângulos é igual a b² + a²;
5. Desenha-se agora o mesmo quadrado de lado b + a, mas coloca-se os quatro triângulos retângulos noutra posição dentro do quadrado: a posição que deixa desocupada uma região que é um quadrado de lado c.
6. Assim, a área da região formada quando os quatro triângulos retângulos são retirados é igual a c².
Como b² + a² representa a área do quadrado maior subtraída da soma das áreas dos triângulos retângulos, e c² representa a mesma área, então b² + a² = c². Ou seja: num triângulo retângulo o quadrado da hipotenusa é igual à soma dos quadrados dos catetos.
Adaptado. Disponível em: https://bit.ly/2QiNr3C
Leia o texto 'Teorema de Pitágoras' e, em seguida, analise as afirmativas abaixo:
I. De acordo com o texto, na geometria euclidiana, o teorema de Pitágoras afirma que, em qualquer triângulo retângulo, o quadrado do comprimento da hipotenusa é igual à soma dos quadrados dos comprimentos dos catetos.
II. O teorema de Pitágoras é uma relação matemática entre os comprimentos dos lados de qualquer triângulo isósceles, de acordo com o texto.
III. O 6º passo para a demonstração do teorema de Pitágoras utilizando a comparação de áreas, de acordo com o texto, é verificar que a área da região formada quando os quatro triângulos retângulos são retirados é igual a c², de acordo com o texto.
Marque a alternativa CORRETA:
I. De acordo com o texto, na geometria euclidiana, o teorema de Pitágoras afirma que, em qualquer triângulo retângulo, o quadrado do comprimento da hipotenusa é igual à soma dos quadrados dos comprimentos dos catetos.
II. O teorema de Pitágoras é uma relação matemática entre os comprimentos dos lados de qualquer triângulo isósceles, de acordo com o texto.
III. O 6º passo para a demonstração do teorema de Pitágoras utilizando a comparação de áreas, de acordo com o texto, é verificar que a área da região formada quando os quatro triângulos retângulos são retirados é igual a c², de acordo com o texto.
Marque a alternativa CORRETA:
-
A) Nenhuma afirmativa está correta.
B) Apenas uma afirmativa está correta.
C) Apenas duas afirmativas estão corretas.
D) Todas as afirmativas estão corretas.
Teorema de Pitágoras
O teorema de Pitágoras é uma relação matemática entre os comprimentos dos lados de qualquer triângulo retângulo. Na geometria euclidiana, o teorema afirma que em qualquer triângulo retângulo, o quadrado do comprimento da hipotenusa é igual à soma dos quadrados dos comprimentos dos catetos.
Por definição, a hipotenusa é o lado oposto ao ângulo reto, e os catetos são os dois lados que o formam. Assim, o teorema de Pitágoras também pode ser enunciado como uma relação entre áreas: em qualquer triângulo retângulo, a área do quadrado cujo lado é a hipotenusa é igual à soma das áreas dos quadrados cujos lados são os catetos.
Para ambos os enunciados anteriormente mencionados, pode-se equacionar: c² = b² + a², onde c representa o comprimento da hipotenusa, e a e b representam os comprimentos dos outros dois lados.
A demonstração do teorema de Pitágoras utilizando a comparação de áreas pode ser feita da seguinte forma:
1. Desenha-se um quadrado de lado b + a;
2. Subdivide-se este quadrado em quatro retângulos, sendo dois deles quadrados de lados, respectivamente, a e b: Traça-se dois segmentos de reta paralelos a dois lados consecutivos do quadrado, sendo cada um deles interno ao quadrado e com o mesmo comprimento que o lado do quadrado;
3. Divide-se cada um destes dois retângulos em dois triângulos retângulos, traçando-se as diagonais. Chama-se c o comprimento de cada diagonal;
4. A área da região que resta ao retirar-se os quatro triângulos retângulos é igual a b² + a²;
5. Desenha-se agora o mesmo quadrado de lado b + a, mas coloca-se os quatro triângulos retângulos noutra posição dentro do quadrado: a posição que deixa desocupada uma região que é um quadrado de lado c.
6. Assim, a área da região formada quando os quatro triângulos retângulos são retirados é igual a c².
Como b² + a² representa a área do quadrado maior subtraída da soma das áreas dos triângulos retângulos, e c² representa a mesma área, então b² + a² = c². Ou seja: num triângulo retângulo o quadrado da hipotenusa é igual à soma dos quadrados dos catetos.
Adaptado. Disponível em: https://bit.ly/2QiNr3C
Leia o texto 'Teorema de Pitágoras' e, em seguida, analise as afirmativas abaixo:
I. No texto, o 2º passo para a demonstração do teorema de Pitágoras utilizando a comparação de áreas exige que o quadrado seja subdividido em quatro retângulos, sendo dois deles quadrados de lados, respectivamente, a e b. Assim, deve-se traçar dois segmentos de reta paralelos a dois lados consecutivos do quadrado, sendo cada um deles interno ao quadrado e com o mesmo comprimento que o lado do quadrado, de acordo com o texto.
II. O 3º passo para a demonstração do teorema de Pitágoras utilizando a comparação de áreas, de acordo com o texto, é dividir cada um dos dois retângulos em dois triângulos retângulos, traçando-se as diagonais. Nesse caso, chama-se c o comprimento de cada diagonal.
III. O 1º passo para a demonstração do teorema de Pitágoras utilizando a comparação de áreas é desenhar um cubo de lado b + a, de acordo com o texto.
Marque a alternativa CORRETA:
I. No texto, o 2º passo para a demonstração do teorema de Pitágoras utilizando a comparação de áreas exige que o quadrado seja subdividido em quatro retângulos, sendo dois deles quadrados de lados, respectivamente, a e b. Assim, deve-se traçar dois segmentos de reta paralelos a dois lados consecutivos do quadrado, sendo cada um deles interno ao quadrado e com o mesmo comprimento que o lado do quadrado, de acordo com o texto.
II. O 3º passo para a demonstração do teorema de Pitágoras utilizando a comparação de áreas, de acordo com o texto, é dividir cada um dos dois retângulos em dois triângulos retângulos, traçando-se as diagonais. Nesse caso, chama-se c o comprimento de cada diagonal.
III. O 1º passo para a demonstração do teorema de Pitágoras utilizando a comparação de áreas é desenhar um cubo de lado b + a, de acordo com o texto.
Marque a alternativa CORRETA:
-
A) Nenhuma afirmativa está correta.
B) Apenas uma afirmativa está correta.
C) Apenas duas afirmativas estão corretas.
D) Todas as afirmativas estão corretas.
Teorema de Pitágoras
O teorema de Pitágoras é uma relação matemática entre os comprimentos dos lados de qualquer triângulo retângulo. Na geometria euclidiana, o teorema afirma que em qualquer triângulo retângulo, o quadrado do comprimento da hipotenusa é igual à soma dos quadrados dos comprimentos dos catetos.
Por definição, a hipotenusa é o lado oposto ao ângulo reto, e os catetos são os dois lados que o formam. Assim, o teorema de Pitágoras também pode ser enunciado como uma relação entre áreas: em qualquer triângulo retângulo, a área do quadrado cujo lado é a hipotenusa é igual à soma das áreas dos quadrados cujos lados são os catetos.
Para ambos os enunciados anteriormente mencionados, pode-se equacionar: c² = b² + a², onde c representa o comprimento da hipotenusa, e a e b representam os comprimentos dos outros dois lados.
A demonstração do teorema de Pitágoras utilizando a comparação de áreas pode ser feita da seguinte forma:
1. Desenha-se um quadrado de lado b + a;
2. Subdivide-se este quadrado em quatro retângulos, sendo dois deles quadrados de lados, respectivamente, a e b: Traça-se dois segmentos de reta paralelos a dois lados consecutivos do quadrado, sendo cada um deles interno ao quadrado e com o mesmo comprimento que o lado do quadrado;
3. Divide-se cada um destes dois retângulos em dois triângulos retângulos, traçando-se as diagonais. Chama-se c o comprimento de cada diagonal;
4. A área da região que resta ao retirar-se os quatro triângulos retângulos é igual a b² + a²;
5. Desenha-se agora o mesmo quadrado de lado b + a, mas coloca-se os quatro triângulos retângulos noutra posição dentro do quadrado: a posição que deixa desocupada uma região que é um quadrado de lado c.
6. Assim, a área da região formada quando os quatro triângulos retângulos são retirados é igual a c².
Como b² + a² representa a área do quadrado maior subtraída da soma das áreas dos triângulos retângulos, e c² representa a mesma área, então b² + a² = c². Ou seja: num triângulo retângulo o quadrado da hipotenusa é igual à soma dos quadrados dos catetos.
Adaptado. Disponível em: https://bit.ly/2QiNr3C
Leia o texto 'Teorema de Pitágoras' e, em seguida, analise as afirmativas abaixo:
I. Segundo o texto, o 4º passo para a demonstração do teorema de Pitágoras utilizando a comparação de áreas é verificar que a área da região que resta, ao retirar-se os quatro triângulos retângulos, é igual a b² a².
II. Como b² + a² representa a área do quadrado maior somada às áreas dos triângulos retângulos, e c² representa a mesma área, então b² + a² = c², de acordo com o texto.
III. Por definição, a hipotenusa é o lado oposto ao ângulo agudo, e os catetos são os dois lados que o formam, de acordo com o texto.
Marque a alternativa CORRETA:
I. Segundo o texto, o 4º passo para a demonstração do teorema de Pitágoras utilizando a comparação de áreas é verificar que a área da região que resta, ao retirar-se os quatro triângulos retângulos, é igual a b² a².
II. Como b² + a² representa a área do quadrado maior somada às áreas dos triângulos retângulos, e c² representa a mesma área, então b² + a² = c², de acordo com o texto.
III. Por definição, a hipotenusa é o lado oposto ao ângulo agudo, e os catetos são os dois lados que o formam, de acordo com o texto.
Marque a alternativa CORRETA:
-
A) Nenhuma afirmativa está correta.
B) Apenas uma afirmativa está correta.
C) Apenas duas afirmativas estão corretas.
D) Todas as afirmativas estão corretas.


