Questões sobre Trinômio do 2º grau

A função do 2º grau y = ax² -– 4x –- 16 apresenta uma de suas raízes igual a 4. A outra raiz é

• A.

  1

• B.

  -1

• C.

  2

• D.

  -2

• E.

  3

O maior número inteiro que pertence ao conjunto imagem da função f(x) = – x² -– 6x + 7 é

• A.

  2

• B.

  18

• C.

  -3

• D.

  16

• E.

  -6

O gráfico a seguir apresenta as raízes e as coordenadas do vértice de uma função do 2º grau da forma y = ax² + bx + c. Assim, a soma dos coeficientes a,b e c desta função é

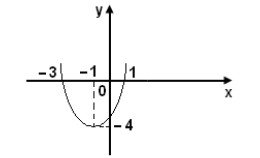
• A.

  -1

• B.

  0

• C.

  1

• D.

  3

• E.

  2

O conjunto solução da inequação x² -– 9x + 20 < 0 apresenta quantas soluções inteiras?

• A.

  Uma única.

• B.

  Três.

• C.

  Duas.

• D.

  Nenhuma.

• E.

  Infinitas.

O valor de k para que a função f(x ) = x² - 2x - 3k tenha como valor máximo -16 é

• A.

  4

• B.

  3

• C.

  5

• D.

  2

• E.

  1

Uma das raízes da equação x² + bx –- 15 = 0 é igual a -– 5. Os valores de b e da outra raiz são, respectivamente

• A.

  –- 2 e 3

• B.

  3 e 2

• C.

  2 e 3

• D.

  3 e -– 2

• E.

  2 e -– 3

A metrologia anunciou que o dia de amanhã será frio, com algumas pancadas de chuva. A temperatura mínima prevista é A e a temperatura máxima é B. Sabendo que A e B são as raízes da equação x² - 26x + 160 = 0, podemos afirmar que A e B são respectivamente, em graus Celsius.

• A.

  10° e 16°.

• B.

  12° e 16°.

• C.

  10° e 18°.

• D.

  15° e 17°.

• E.

  12° e 18°.

Após diversos dias de pesquisa, uma equipe médica chegou à função A(x) = - x² + 10x -16 que retorna o aproveitamento (em pontos) de um atleta, e que x é o tempo treinado em horas. Quantas horas de treino são necessárias para que o referido atleta alcance o auge de seu desempenho?

• A.

  1 hora.

• B.

  3 horas.

• C.

  5 horas.

• D.

  7 horas.

• E.

  9 horas.

O arco de parábola representado pela função, onde h representa a altura em metros e t o tempo em segundos, descreve a trajetória de um grilo ao saltar. Assim, podemos concluir que a altura máxima atingida pelo grilo, em metros, é

• A.

  0,50

• B.

  0,75

• C.

  1,00

• D.

  1,25

• E.

  1,50

Uma professora de 9º ano elaborou uma prova em que uma das questões era a resolução de uma equação do 2º grau. No dia da aplicação da prova, por falha da reprografia, um dos coeficientes da equação saiu borrado. Sabendo que a equação da prova era 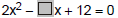e que a professora sabia que as raízes desta equação eram iguais a 2 e 3, podemos concluir que o número que está faltando é o

• A.

  5

• B.

  6

• C.

  8

• D.

  10

• E.

  12