Questões sobre Trinômio do 2º grau

Assinale a função que NÃO apresenta raízes reais e cujo gráfico intercepta o eixo das ordenadas em um ponto de ordenada negativa

• A.

  y = 2x² – 4x + 3

• B. y = x² + 2x – 1
• C.

  y = – x² + 7x – 12

• D.

  y = – x² + 2x – 5

• E.

  y = 6x² + x – 1

Uma das raízes da equação x² + bx -– 15 = 0 é igual a – 5. Os valores de b e da outra raiz são, respectivamente

• A.

  – -2 e 3

• B.

  3 e 2

• C.

  2 e 3

• D.

  3 e –-2

• E.

  2 e – -3

Uma indústria fabrica somente os produtos X e Y e sua produção é totalmente vendida. O preço unitário de venda de X é igual a 4 unidades monetárias e de Y igual a 3 unidades monetárias. Sabe-se que a indústria opera segundo a restrição x² + y² = 10.000, em que x e y indicam, respectivamente, as quantidades fabricadas de X e Y. Existe uma quantidade fabricada de X e uma quantidade fabricada de Y, que maximiza a receita de vendas. O valor desta receita, em unidades monetárias, é igual a

• A.

  800.

• B.

  720.

• C.

  600.

• D.

  500.

• E.

  480.

Sendo x um elemento do conjunto dos números reais, qual é o conjunto solução da inequação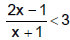

• A.

  S = [ -4 , -1 ].

• B.

  

• C.

  

• D.

  

• E.

  

As quantidades de empregados de três empresas são números positivos distintos que satisfazem, simultaneamente, às inequações x² - 5x + 4 > 0 e 2x - 16 < 0. Nesse caso, é correto afirmar que

as três empresas têm, juntas, 18 empregados.

• C. Certo
• E. Errado

As quantidades de empregados de três empresas são números positivos distintos que satisfazem, simultaneamente, às inequações x² - 5x + 4 > 0 e 2x - 16 < 0. Nesse caso, é correto afirmar que

o produto dos números correspondentes às quantidades de empregados dessas três empresas é igual 240.

• C. Certo
• E. Errado

A partir das funções f(x) = x²  - 2x - 3 e g(x) = m(x - 1), em que a variável x e a constante m são reais, julgue os itens subsequentes, a respeito de seus gráficos em um sistema de coordenadas cartesianas ortogonais xOy.

Se m = 3, então os gráficos dessas funções se interceptam em pontos cujas abscissas são números racionais não inteiros.

• C. Certo
• E. Errado

A partir das funções f(x) = x²  - 2x - 3 e g(x) = m(x - 1), em que a variável x e a constante m são reais, julgue os itens subsequentes, a respeito de seus gráficos em um sistema de coordenadas cartesianas ortogonais xOy.

Independentemente do valor de m, os gráficos dessas funções se interceptam em 2 pontos distintos.

• C. Certo
• E. Errado

O gráfico cartesiano abaixo representa uma função g(x) = 2x² + kx + m, em que k e m são números reais.

O resultado de m + k é igual a:

• A.

  −26.

• B.

  −14.

• C.

  −12.

• D.

  −8.

• E.

  −6.

Sendo x e y números reais tais que y = − 6x² +11x − 4 , o valor mínimo de x para o qual o valor correspondente de y é máximo é

• A.

  2/3.

• B.

  3/4.

• C.

  5/6.

• D.

  11/12.

• E.

  1.