Questões de Matemática da Centro de Seleção e de Promoção de Eventos UnB (CESPE)
Lista completa de Questões de Matemática da Centro de Seleção e de Promoção de Eventos UnB (CESPE) para resolução totalmente grátis. Selecione os assuntos no filtro de questões e comece a resolver exercícios.
Considere que o lucro em reais de uma loja, pela venda diária de x peças, seja dado por 150 × L(x), em que L(x) = (12 - x)(x - 6), e que quando L(x) < 0, a loja tem prejuízo ao vender x peças. Com base nessas informações, julgue os itens que se seguem.
O lucro diário máximo é obtido com a venda de 10 peças.
- C. Certo
- E. Errado

No ano em que começou a atuação dos agentes comunitários referidos no texto, o número de processos ajuizados diminuiu consideravelmente na cidade de Ceilândia. Suponha-se que, nesse ano, P(t) e F(t) correspondam, respectivamente, ao número total de processos e ao número desses processos relacionados à justiça da família ajuizados no TJDFT no mês t. Suponha-se que P(t) = -10t2 + 100t + 600 e que F(t) = 720 - 30t, com em que t = 1 corresponde ao mês de janeiro, t = 2 corresponde a fevereiro, e assim por diante.
Com base nessas informações, julgue os itens seguintes, referentes ao ano inicial de atuação dos agentes.
O gráfico a seguir ilustra corretamente o comportamento de P(t) ao longo do tempo t, para .
- C. Certo
- E. Errado
 Com base no texto e na tabela, na região mencionada, o número total de filhos das famílias que exercem atividade rural e recebem bolsa do PETI é
Com base no texto e na tabela, na região mencionada, o número total de filhos das famílias que exercem atividade rural e recebem bolsa do PETI é
- A. inferior a 180.
- B. superior a 181 e inferior a 185.
- C. superior a 186 e inferior a 190.
- D. superior a 191.
Matemática - Análise Combinatória Simples - Centro de Seleção e de Promoção de Eventos UnB (CESPE) - 2008
Com relação a probabilidade, combinações, arranjos e permutações, julgue os seguintes itens.
Sabe-se que, no Brasil, as placas de identificação dos veículos têm 3 letras do alfabeto e 4 algarismos, escolhidos de 0 a 9. Então, seguindo-se essa mesma lei de formação, mas utilizando-se apenas as letras da palavra BRASIL, é possível construir mais de 600.000 placas diferentes que não possuam letras nem algarismos repetidos.
- C. Certo
- E. Errado
Matemática - Números reais e complexos - Centro de Seleção e de Promoção de Eventos UnB (CESPE) - 2008
Considere os itens a seguir os quais contêm o resultado de uma operação realizada a partir de dois números irracionais positivos x e y.
I. x + y
II. x - y
III. x × y
IV. ![]()
V. xy
É correto afirmar que, independentemente dos valores de x e y, o resultado da operação é sempre um número irracional
- A.
em nenhum dos itens.
- B.
apenas no item III.
- C.
apenas no item IV.
- D.
apenas no item V.

No ano em que começou a atuação dos agentes comunitários referidos no texto, o número de processos ajuizados diminuiu consideravelmente na cidade de Ceilândia. Suponha-se que, nesse ano, P(t) e F(t) correspondam, respectivamente, ao número total de processos e ao número desses processos relacionados à justiça da família ajuizados no TJDFT no mês t. Suponha-se que P(t) = -10t2 + 100t + 600 e que F(t) = 720 - 30t, com em que t = 1 corresponde ao mês de janeiro, t = 2 corresponde a fevereiro, e assim por diante.
Com base nessas informações, julgue os itens seguintes, referentes ao ano inicial de atuação dos agentes.
Em determinado mês do ano inicial de atuação dos agentes, o número total de processos ajuizados foi igual a 600.
- C. Certo
- E. Errado
Certa quantia em reais foi dividida entre três irmãos. Um deles ficou com o restante. Então, o terceiro ficou com uma fração da quantia igual a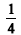 da quantia, outro ficou com
da quantia, outro ficou com 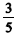 e o terceiro, com
e o terceiro, com
- A.

- B.

- C.

- D.

Matemática - Números reais e complexos - Centro de Seleção e de Promoção de Eventos UnB (CESPE) - 2008
Julgue os itens a seguir.
I Existem números naturais que não são números inteiros.
II A cada número inteiro corresponde outro número inteiro que, somado ao primeiro, dá como resultado o número zero.
III Todo número racional é um número real.
IV O número real representado pela dízima periódica 0,333... não é um número racional.
Estão certos apenas os itens
- A. I e III.
- B. I e IV.
- C. II e III.
- D. II e IV.

No ano em que começou a atuação dos agentes comunitários referidos no texto, o número de processos ajuizados diminuiu consideravelmente na cidade de Ceilândia. Suponha-se que, nesse ano, P(t) e F(t) correspondam, respectivamente, ao número total de processos e ao número desses processos relacionados à justiça da família ajuizados no TJDFT no mês t. Suponha-se que P(t) = -10t2 + 100t + 600 e que F(t) = 720 - 30t, com em que t = 1 corresponde ao mês de janeiro, t = 2 corresponde a fevereiro, e assim por diante.
Com base nessas informações, julgue os itens seguintes, referentes ao ano inicial de atuação dos agentes.
Nesse ano, maio — t = 5 — foi o mês em que mais processos foram ajuizados.
- C. Certo
- E. Errado
O valor numérico da expressão 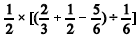 é igual a
é igual a
- A.

- B.
1.
- C.

- D.
2.


