Questões de Matemática da Centro de Seleção e de Promoção de Eventos UnB (CESPE)

Os números a₃, a₅, e a₆ formam, nessa ordem, uma progressão aritmética.

• C. Certo
• E. Errado

Uma preocupação de todos os governantes é a busca por fontes alternativas de energia que possam diminuir a dependência mundial do petróleo. Suponha que o consumo de petróleo por todo o planeta, em milhões de barris diários, possa ser estimado pela equação 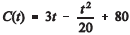 , em que t = 0 corresponde ao ano de 2004, t = 1, ao ano de 2005, e assim sucessivamente. Com base nessa estimativa, julgue os itens a seguir.

No ano de 2070, o consumo mundial de petróleo retornará a um nível de consumo igual ao de 2004.

• C. Certo
• E. Errado

Para seus profissionais de nível superior, uma empresa paga salários mensais de R$ 3.800,00; para os de nível médio, o salário mensal pago pela empresa é de R$ 1.800,00. A empresa possui 30 profissionais desses dois níveis e a despesa mensal com os salários desses profissionais é uma quantia que está entre R$ 63.000,00 e R$ 65.000,00. Com base nessas informações, julgue os itens seguintes.

O número de profissionais de nível superior dessa empresa é um número primo.

• C. Certo
• E. Errado

Uma preocupação de todos os governantes é a busca por fontes alternativas de energia que possam diminuir a dependência mundial do petróleo. Suponha que o consumo de petróleo por todo o planeta, em milhões de barris diários, possa ser estimado pela equação 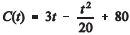 , em que t = 0 corresponde ao ano de 2004, t = 1, ao ano de 2005, e assim sucessivamente. Com base nessa estimativa, julgue os itens a seguir.

O consumo mundial de petróleo atingirá seu pico máximo antes do ano de 2035.

• C. Certo
• E. Errado

Com relação a equações do 1.º grau, julgue os itens a seguir.

Sabe-se que, quando a terça parte de um número é somada à sua quinta parte, obtém-se como resultado o número 16. Nesse caso, é correto afirmar que esse número é menor que 35.

• C. Certo
• E. Errado

O problema apresentado a seguir, encontrado no Papiro Matemático Rhind ou Ahmos - 1650 a.C -, envolve a noção de progressão aritmética.

"Divida 100 pães por 5 homens, de modo que as quantidades recebidas por cada um estejam em progressão aritmética e que a soma das duas quantidades menores seja igual a 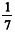da soma das outras três."

 Com base nessas informações e designando por a o termo inicial e por r a razão da progressão aritmética, julgue os itens a seguir.

Desconsiderando as hipóteses do problema egípcio, dividindo os 100 pães entre os 5 homens de forma que as quantidades recebidas por cada um estejam em uma progressão aritmética de razão 3, então o número máximo de pães que um dos homens receberia é igual a 29.

• C. Certo
• E. Errado

Uma preocupação de todos os governantes é a busca por fontes alternativas de energia que possam diminuir a dependência mundial do petróleo. Suponha que o consumo de petróleo por todo o planeta, em milhões de barris diários, possa ser estimado pela equação 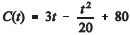 , em que t = 0 corresponde ao ano de 2004, t = 1, ao ano de 2005, e assim sucessivamente. Com base nessa estimativa, julgue os itens a seguir.

Em 2009, o consumo mundial de petróleo será superior a 93 milhões de barris diários.

• C. Certo
• E. Errado

Em um sistema de coordenadas cartesianas ortogonais xOy, considere o conjunto dos pares (x, y) que satisfazem à equação 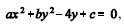 em que a, b e c são números reais fixos, Nesse caso,

se a = b = 1 e c = 3, então a equação acima representa uma circunferência de centro no ponto de coordenadas (0, 2) e raio 1.

• C. Certo
• E. Errado

Um motorista, após ter enchido o tanque de seu veículo, gastou 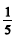da capacidade do tanque para chegar à cidade A; gastou mais 28 L para ir da cidade A até a cidade B; sobrou, no tanque, uma quantidade de combustível que corresponde a  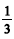de sua capacidade. Com base nessas informações, julgue os itens a seguir.

Quando o veículo chegou à cidade B, havia, no tanque menos de 21 L de combustível.

• C. Certo
• E. Errado

O problema apresentado a seguir, encontrado no Papiro Matemático Rhind ou Ahmos - 1650 a.C -, envolve a noção de progressão aritmética.

"Divida 100 pães por 5 homens, de modo que as quantidades recebidas por cada um estejam em progressão aritmética e que a soma das duas quantidades menores seja igual a 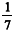da soma das outras três."

 Com base nessas informações e designando por a o termo inicial e por r a razão da progressão aritmética, julgue os itens a seguir.

Se b = a, b = a + r, b = a + 2r, b = a + 3r e b = a + 4r são os cinco termos da progressão aritmética, então b3 + b4 + b5 = 3 (b3 + r).

• C. Certo
• E. Errado