Questões de Matemática da Centro de Seleção e de Promoção de Eventos UnB (CESPE)

A respeito de uma função f(x) tal que g(x) = 3x² - 6x - 9 é a função derivada de f, assinale a opção correta.

• A.

  x = 3 é ponto de máximo local de f.

• B.

  x = 1 é ponto de inflexão de f.

• C.

  

• D.

  f possui três pontos críticos.

• E.

  x = 1 é ponto de mínimo local de f.

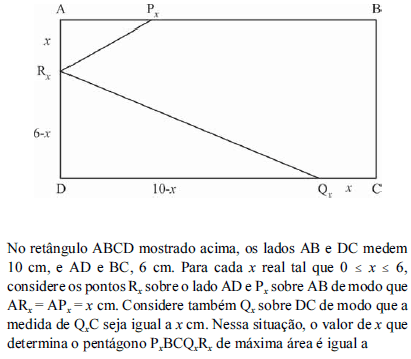
• A.

  1.

• B.

  2.

• C.

  3.

• D.

  4.

• E.

  5.

A numeração das notas de papel-moeda de determinado país é constituída por duas das 26 letras do alfabeto da língua portuguesa, com ou sem repetição, seguidas de um numeral com 9 algarismos arábicos, de 0 a 9, com ou sem repetição. Julgue os próximos itens, relativos a esse sistema de numeração.

Existem mais de 700 formas diferentes de se escolher as duas letras que iniciarão a numeração de uma nota.

• C. Certo
• E. Errado

A numeração das notas de papel-moeda de determinado país é constituída por duas das 26 letras do alfabeto da língua portuguesa, com ou sem repetição, seguidas de um numeral com 9 algarismos arábicos, de 0 a 9, com ou sem repetição. Julgue os próximos itens, relativos a esse sistema de numeração.

Considere que, até o ano 2000, as notas de papel-moeda desse país fossem retangulares e medissem 14 cm × 6,5 cm e que, a partir de 2001, essas notas tivessem passado a medir 12,8 cm × 6,5 cm, mas tivessem mantido a forma retangular. Nesse caso, com o papel-moeda gasto para se fabricar 10 notas de acordo com as medidas adotadas antes de 2000 é possível fabricar 11 notas conforme as medidas determinadas após 2001.

• C. Certo
• E. Errado

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

No polinômio (x + 1)²⁰⁰, o coeficiente do termo x⁵⁰ é igual a

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

O último teorema de Fermat, enunciado em 1637 por Pierre de Fermat, foi provado, em 1995, pelo matemático britânico Andrew Wiles. O referido teorema assevera que não existem números inteiros não nulos x, y, z e n, com n > 2, de modo que xⁿ + yⁿ = zⁿ. Considere que a, b e c sejam números racionais positivos que constituem as medidas dos três lados de um triangulo retângulo. Nessa situação, a partir do referido teorema de Fermat e de propriedades dos números reais, assinale a opção correta.

• A.

  Se a² + b² = c², em que a = k, b = k + 2 e c = k + 4, e k > 0 é um número inteiro, então, necessariamente, k > 10.

• B.

  Pelo menos um dos números a², b² ou c² é um número irracional.

• C.

  

• D.

  Se a for um número inteiro, então a > b + c.

• E.

  Se a e b forem números inteiros ímpares e se a² + b² = c², então c também será ímpar.

• A.

  

• B.

  [ln(2)]⁴ s.

• C.

  ln(2⁴) s.

• D.

  

• E.

  0 s.

Se a e b são números reais, define-se, a partir de a e b, uma sequência de Fibonacci {ak} por: a₁ = a, a₂ = b, e a_k = a_{k – 1} + a_{k – 2}, para k > 2. Nesse sentido, é correto afirmar que

• A.

  apenas {x_k} é uma sequência de Fibonacci.

• B.

  apenas {y_k} é uma sequência de Fibonacci.

• C.

  apenas {x_k} e {y_k} são sequências de Fibonacci.

• D.

  apenas {x_k} e {z_k} são sequências de Fibonacci.

• E.

  {x_k}, {y_k} e {z_k} são sequências de Fibonacci.

Se 2 anos após a semeadura haviam 20, 15 e 29 pés da planta nos jardins X, Y e Z, respectivamente, então, no jardim Y foram semeadas

• A.

  2 sementes.

• B.

  5 sementes.

• C.

  7 sementes.

• D.

  10 sementes.

• E.

  16 sementes.