Questões de Matemática da Fundação Universa (FUNIVERSA)

Considere que a secretaria de uma escola gaste mensalmente 600 folhas de papel A4. Essa escola atende a 350 estudantes de nível fundamental, distribuídos nos períodos matutino e vespertino. O espaço da escola que estava ocioso no período noturno passará a atender 200 estudantes de nível médio. Considere, ainda, que o consumo de papel A4 em uma escola de nível médio corresponda a 70% do consumo de uma escola de nível fundamental com a mesma quantidade de alunos. Nessa situação, o consumo total mensal de papel A4 na secretaria da escola passará a ser de

• A.

  240 folhas.

• B.

  400 folhas.

• C.

  660 folhas.

• D.

  660 folhas.

• E.

  940 folhas.

Utilizando o método iterativo para resolver a equação 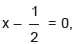 e iniciando pelo número 2, assinale a alternativa que apresenta a quantidade de tentativas que serão necessárias para encontrar a raiz dessa equação.

• A.

  3

• B.

  4

• C.

  5

• D.

  6

• E.

  7

• A.

  reflexão na origem.

• B.

  reflexão em torno do eixo x.

• C.

  rotação no sentido anti-horário em torno da origem.

• D.

  rotação no sentido horário em torno da origem.

• E.

  translação em torno da origem.

Identifique a equação que corresponde a um hiperboloide de uma folha.

• A.

  x² + 3y² + z² = 3

• B.

  3x² + 3y² + 3z² - 2 = 0

• C.

  -3x² - 3y² + z² = 3

• D.

  x² - 3y² + 2z² = 8

• E.

  x² + 2y² - 4z² = 0

Um reagente químico é comercializado em pacotes de 3 kg. Ao receber um desses pacotes, um agente deve distribuir seu conteúdo em frascos. Os frascos têm capacidade de 1 kg, 2 kg e 3 kg e encontram-se vazios. Para que a quantidade recebida seja distribuída de forma proporcional nos frascos, o agente deve colocar, em cada um deles, uma quantidade proporcional à capacidade do frasco. Dessa forma, a distribuição correta do conteúdo do pacote é aquela na qual se deposita, no maior dos frascos,

• A.

  0,5 kg do reagente.

• B.

  1,0 kg do reagente.

• C.

  1,5 kg do reagente.

• D.

  2,0 kg do reagente.

• E.

  2,5 kg do reagente.

Para o registro de um caso, o agente auxiliar é incumbido do preenchimento de um formulário. Verificou-se que um auxiliar gastou 4 horas para preencher 20 desses formulários. Nessas condições, é correto concluir que dois outros auxiliares que têm o dobro da eficiência do primeiro preencherão 50 desses formulários em

• A.

  2 horas e 30 minutos.

• B.

  5 horas.

• C.

  10 horas.

• D.

  20 horas.

• E.

  40 horas.

Para revestir externamente quatro caixas com faces retangulares, um agente usou seis folhas de papel adesivo, sem sobras e sem sobreposição do papel. No mês seguinte, o agente recebeu outras seis caixas com faces retangulares. O agente verificou que as medidas lineares das novas caixas correspondem, respectivamente, ao dobro das medidas lineares das caixas anteriores. Dessa forma, o total de folhas de papel adesivo, iguais às anteriores, que o agente deverá usar para revestir essas novas caixas, como fez com as primeiras, é igual a

• A.

  9.

• B.

  12.

• C.

  18.

• D.

  24.

• E.

  36.

Para revestir externamente quatro caixas com faces retangulares, um agente usou seis folhas de papel adesivo, sem sobras e sem sobreposição do papel. No mês seguinte, o agente recebeu outras seis caixas com faces retangulares. O agente verificou que as medidas lineares das novas caixas correspondem, respectivamente, ao dobro das medidas lineares das caixas anteriores. Dessa forma, o total de folhas de papel adesivo, iguais às anteriores, que o agente deverá usar para revestir essas novas caixas, como fez com as primeiras, é igual a

• A.

  9.

• B.

  12.

• C.

  18.

• D.

  24.

• E.

  36.

Sabe-se que a função f(x) = sen x é uma função ímpar, enquanto a função g(x) = cos x é uma função par. Dada a equação: cos x × cos (–x) – sen (–x) × sen x = tg x, verifica-se que uma das soluções dela é igual a

• A.

  0.

• B.

  

• C.

  

• D.

  

• E.

  

Se a e b correspondem aos valores que atendem simultaneamente às equações 2ª + 3^b = 17 e 2^a+2 – 3^{b – 1} = 29, então o valor de (2b)^a é igual a

• A.

  12.

• B.

  16.

• C.

  32.

• D.

  36.

• E.

  64.