Questões de Raciocínio lógico do ano 2005
Lista completa de Questões de Raciocínio lógico do ano 2005 para resolução totalmente grátis. Selecione os assuntos no filtro de questões e comece a resolver exercícios.
Raciocínio lógico - Tautologia e Contradição - Centro de Seleção e de Promoção de Eventos UnB (CESPE) - 2005
Considere a proposição: Se meu cliente fosse culpado, então a arma do crime estaria no carro. Simbolizando por P o trecho meu cliente fosse culpado e simbolizando por Q o trecho a arma estaria no carro, obtém-se uma proposição implicativa, ou simplesmente uma implicação, que é lida: Se P então Q, e simbolizada por P → Q. Uma tautologia é uma proposição que é sempre V (verdadeira). Uma proposição que tenha a forma P → Q é V sempre que P for F (falsa) e sempre que P e Q forem V. Com base nessas informações e na simbolização sugerida, julgue os itens subseqüentes.
A proposição "Se meu cliente fosse culpado, então a arma do crime estaria no carro. Portanto, se a arma do crime não estava no carro, então meu cliente não é culpado." é uma tautologia.
- C. Certo
- E. Errado
Raciocínio lógico - Silogismo: Todo, Algum e Nenhum - Centro de Seleção e de Promoção de Eventos UnB (CESPE) - 2005
Considerando os argumentos I e II acima, julgue os próximos itens.
O argumento II é válido porque toda vez que as premissas P1 e P2 forem verdadeiras, então a conclusão também será verdadeira.
- C. Certo
- E. Errado
Raciocínio lógico - Silogismo: Todo, Algum e Nenhum - Centro de Seleção e de Promoção de Eventos UnB (CESPE) - 2005
Considerando os argumentos I e II acima, julgue os próximos itens.
O argumento I não é válido porque, mesmo que as premissas P1 e P2 sejam verdadeiras, isto não acarreta que a conclusão seja verdadeira.
- C. Certo
- E. Errado
A afirmação "Não é verdade que, se Pedro está em Roma, então Paulo está em Paris" é logicamente equivalente à afirmação:
- A. É verdade que "Pedro está em Roma e Paulo está em Paris".
- B. Não é verdade que "Pedro está em Roma ou Paulo não está em Paris".
- C. Não é verdade que "Pedro não está em Roma ou Paulo não está em Paris".
- D. Não é verdade que "Pedro não está em Roma ou Paulo está em Paris".
- E. É verdade que "Pedro está em Roma ou Paulo está em Paris".

Considerando as tabelas anteriores, que apresentam informações relativas à população urbana do DF, obtidas na pesquisa distrital por amostra de domicílios realizada em 2004, julgue os próximos itens.
Ao se escolher uma pessoa ao acaso, entre toda a população urbana do DF, a probabilidade de essa pessoa ter menos de 25 anos de idade é superior a 2/5.- C. Certo
- E. Errado
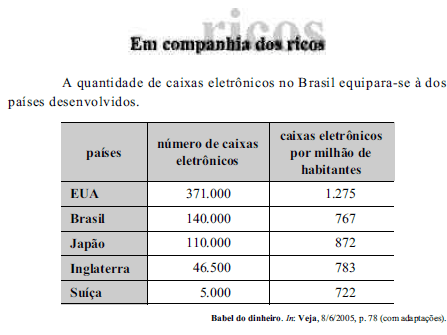
Considerando o texto acima, que contém dados a respeito do número de caixas eletrônicos de bancos, julgue os itens seguintes.
Considere que os cincos países relacionados na tabela possuam caixas eletrônicos diferentes e que todos esses caixas sejam colocados em um grande pátio e, em seguida, retire-se um deles, ao acaso. Então, a probabilidade de que esse caixa retirado seja do Brasil é superior a 0,20.
- C. Certo
- E. Errado
Em uma caixa há oito bolas brancas e duas azuis. Retirase, ao acaso, uma bola da caixa. Após, sem haver recolocado a primeira bola na caixa, retira-se, também ao acaso, uma segunda bola. Verifica-se que essa segunda bola é azul. Dado que essa segunda bola é azul, a probabilidade de que a primeira bola extraída seja também azul é:
- A. 1/3
- B. 2/9
- C. 1/9
- D. 2/10
- E. 3/10
Ana precisa chegar ao aeroporto para buscar uma amiga. Ela pode escolher dois trajetos, A ou B. Devido ao intenso tráfego, se Ana escolher o trajeto A, existe uma probabilidade de 0,4 de ela se atrasar. Se Ana escolher o trajeto B, essa probabilidade passa para 0,30. As probabilidades de Ana escolher os trajetos A ou B são, respectivamente, 0,6 e 0,4. Sabendo-se que Ana não se atrasou, então a probabilidade de ela ter escolhido o trajeto B é igual a:
- a.
6/25
- b.
6/13
- c.
7/13
- d.
7/25
- e.
7/16
Você está à frente de três urnas, cada uma delas contendo duas bolas. Você não pode ver o interior das urnas, mas sabe que em uma delas há duas bolas azuis. Sabe, ainda, que em uma outra urna há duas bolas vermelhas. E sabe, finalmente, que na outra urna há uma bola azul e uma vermelha. Cada urna possui uma etiqueta indicando seu conteúdo, "AA", "VV", "AV" (sendo "A" para bola azul, e "V" para bola vermelha). Ocorre que "e isto você também sabe" alguém trocou as etiquetas de tal forma que todas as urnas estão, agora, etiquetadas erradamente. Você pode retirar uma bola de cada vez, da urna que bem entender, olhar a sua cor, e recolocá-la novamente na urna. E você pode fazer isto quantas vezes quiser. O seu desafio é determinar, por meio desse procedimento, o conteúdo exato de cada urna, fazendo o menor número de retiradas logicamente possível. O número mínimo de retiradas necessárias para você determinar logicamente o conteúdo exato de cada uma das três urnas é:
- a.
1
- b.
2
- c.
3
- d.
4
- e.
5
Há três moedas em um saco. Apenas uma delas é uma moeda normal, com ""cara"" em uma face e ""coroa"" na outra. As demais são moedas defeituosas. Uma delas tem "cara"" em ambas as faces. A outra tem ""coroa"" em ambas as faces. Uma moeda é retirada do saco, ao acaso, e é colocada sobre a mesa sem que se veja qual a face que ficou voltada para baixo. Vê-se que a face voltada para cima é ""cara". Considerando todas estas informações, a probabilidade de que a face voltada para baixo seja ""coroa"" é igual a:
- a.
1/2
- b.
1/3
- c.
1/4
- d.
2/3
- e.
3/4


