Questões de Estatística

O teor de etanol presente na gasolina determina o preço de venda. Seja X a variável aleatória que representa o teor de etanol. Se X está entre 0,20 e 0,25, a gasolina é vendida a R$ 2,00 por litro; caso contrário, a gasolina é vendida a R$ 1,80 por litro. A função de densidade de probabilidade de X é:

O valor esperado do preço de venda, por litro, em reais, é

• A.

  1,95

• B.

  1,93

• C.

  1,88

• D.

  1,84

• E.

  1,81

O coeficiente de determinação do modelo ajustado (R²) é inferior a 40%.

• C. Certo
• E. Errado

Suponha que o custo de produção de energia por kilowatt/hora seja uma função do custo do carvão, em centavos de dólar por milhão de Btu. Os dados foram obtidos a partir de uma amostra da produção de 12 moinhos.

Os valores de P, Q e R que completam as tabelas acima são:

• A.

  P = 0,14 , Q = 5 , R = 5

• B.

  P = 0,14 , Q = 5 , R = 5

• C.

  P = 1,14 , Q = 5 , R = 0,5

• D.

  P = 0,14 , Q = 25 , R = 5

• E.

  P = 1,4 , Q = 25 , R = 0,5

A média aritmética e a variância dos salários dos empre- gados em uma fábrica são iguais a R$ 1.500,00 e 22.500 (R$) ², respectivamente. Para todos os emprega- dos foi concedido um reajuste de 8% e posteriormente um adicional fixo de R$ 180,00. O coeficiente de variação, após o reajuste e o adicional concedidos, é igual a

• A.

  5%.

• B.

  6%.

• C.

  8%.

• D.

  9%.

• E.

  10%.

Leia o texto a seguir para responder às questões de nos 22 e 23.

A média das idades dessas crianças, em anos, é

• A.

  5,0

• B.

  5,2

• C.

  5,4

• D.

  5,6

• E.

  5,8

Texto V, para responder às questões 53 e 54.

 O Teorema Central do Limite é a principal justificativa para o uso da amostragem em problemas que envolvam populações infinitas, ou mesmo em populações finitas, porém, muito grandes quando comparadas ao tamanho da amostra. O resultado de um censo apontou que, em uma cidade com 25.000 famílias, a renda média era de R$ 3.170,00 e o desvio-padrão, de R$ 2.000,00. Um pesquisador utilizou uma amostra aleatória simples de 400 famílias daquela população e obteve média de R$ 3.070,00 com desvio-padrão de R$ 1.920,00.

A probabilidade de se obter uma amostra com média de até R$ 3.070,00 é

• A.

  inferior a 2%.

• B.

  entre 2% e 35%.

• C.

  entre 35% e 50%.

• D.

  entre 50% e 65%.

• E.

  entre 65% e 98%.

Considere que uma variável aleatória tem na população uma distribuição qualquer. Em amostras aleatórias de tamanho n, a distribuição da média amostral tem

• A.

  média e variância iguais às da população.

• B.

  mesma média da população e variância (1/n) vezes a variância populacional.

• C.

  mesma média da população, mas com a variância n vezes maior.

• D.

  distribuição normal com a mesma média e a mesma variância da população.

• E.

  distribuição normal com média zero e variância unitária.

Um assalariado gasta 55% do seu salário com alimentação, aluguel e transporte, sendo 25% com alimentação, 10%, com aluguel e 20% com transporte. Considere-se a hipótese de que, no período de 2007 a 2008, os preços desses itens variaram de acordo com os índices a seguir.

Considerando que não houve aumento de salários nem modificação nas quantidades consumidas, que proporção do salário o trabalhador passou a comprometer com esses três itens?

• A.

  36,50%

• B.

  47,25%

• C.

  55,00%

• D.

  62,85%

• E.

  91,50%

O tempo, em horas, que uma empresa leva para localizar e reparar uma avaria elétrica, em um determinado setor, é uma variável aleatória X, cuja função densidade é dada por:

• A.

  1/3

• B.

  2/5

• C.

  1/2

• D.

  2/3

• E.

  3/4

Seja X uma variável aleatória com função geratriz de momentos

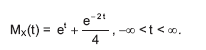
O valor esperado e a variância de X são, respectivamente,

• A.

  1/4 e 3/2

• B.

  1/4 e 3/2

• C.

  1/2 e 7/4

• D.

  1/2 e 3/2

• E.

  1/2 e 2