Questões de Estatística

• A.

  0

• B.

  0,1

• C.

  0,2

• D.

  0,5

• E.

  1

A figura acima corresponde a um diagrama de dispersão entre a variável y (gasto percentual com saúde) e x (renda bruta familiar, em R$ mil), obtida com base em uma amostra de 10 famílias. Com respeito ao ajuste de um modelo de regressão linear simples na forma y = ax + b + g, em que g é o erro aleatório e a e b são os coeficientes do modelo, foram obtidos os seguintes resultados.

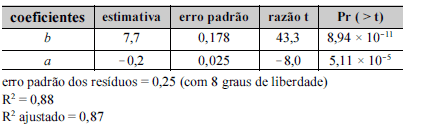
Com base nessas informações, julgue os itens seguintes.

A variância amostral da variável regressora x é inferior a 10.

• C. Certo
• E. Errado

A estimativa da mediana de X é inferior a R$ 700,00.

• C. Certo
• E. Errado

A respeito da distribuição binomial X com parâmetros n e p, em que n 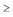 1 e 0 < p < 1, julgue os itens subsequentes.

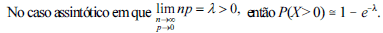
• C. Certo
• E. Errado

Utilizando a formulação de Laspeyres, a variação do índice de preço desse bem no período t em relação ao período 0 é, aproximadamente,

• A.

  22%

• B.

  24%

• C.

  65%

• D.

  122%

• E.

  165%

• A.

  0,20.

• B.

  0,40.

• C.

  0,50.

• D.

  0,55.

• E.

  0,60.

A respeito da distribuição binomial X com parâmetros n e p, em que n 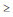 1 e 0 < p < 1, julgue os itens subsequentes.

Considere a seguinte situação hipotética. De uma urna que contém 15 bolas brancas e 1 bola vermelha serão retiradas aleatoriamente 12 bolas. Em cada retirada, será observada a cor da bola selecionada. Se branca, a bola não será devolvida à urna; se vermelha, a bola será devolvida à urna. Ao final do processo, será registrado o número X de vezes que a bola vermelha foi observada nessas doze retiradas. Em face dessa situação, é correto afirmar que X é uma variável aleatória com distribuição binomial com n = 12.

• C. Certo
• E. Errado

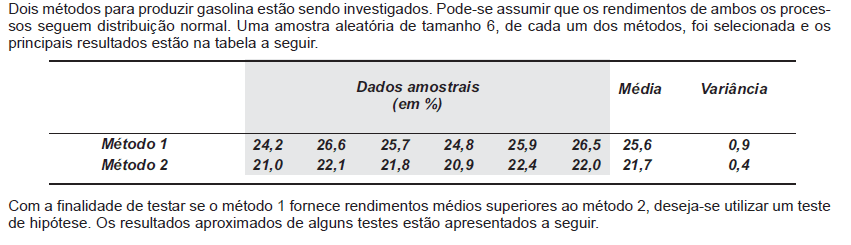
Com os resultados à esquerda e considerando o nível de significância de 10%, conclui-se que a hipótese de igualdade das variâncias (A) não é rejeitada

• A.

  não é rejeitada segundo o teste P e, consequentemente, o teste utilizado para testar a hipótese do rendimento do método 1 ser superior ao do método 2 é o teste Q, que não rejeita a hipótese nula.

• B.

  não é rejeitada segundo o teste P e, consequentemente, o teste utilizado para testar a hipótese do rendimento do método 1 ser superior ao do método 2 é o teste Q, que rejeita a hipótese nula.

• C.

  não é rejeitada segundo o teste P e, consequentemente, o teste utilizado para testar a hipótese do rendimento do método 1 ser superior ao do método 2 é o teste Q, que rejeita a hipótese nula.

• D.

  é rejeitada segundo o teste P e, consequentemente, o teste utilizado para testar a hipótese do rendimento do método 1 ser superior ao do método 2 é o teste Q, que rejeita a hipótese nula.

• E.

  é rejeitada segundo o teste P e, consequentemente, o teste utilizado para testar a hipótese do rendimento do método 1 ser superior ao do método 2, é o teste R, que rejeita a hipótese nula.

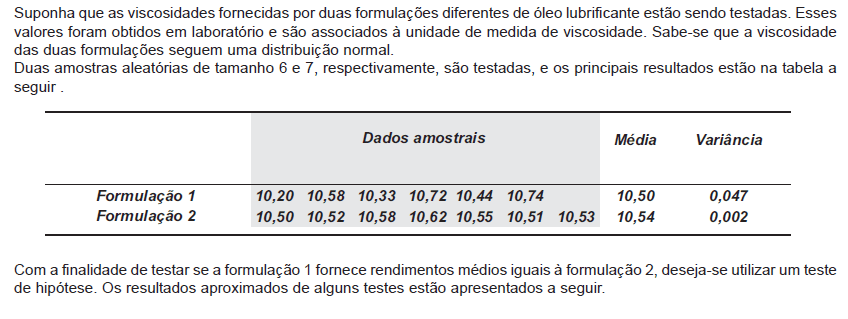
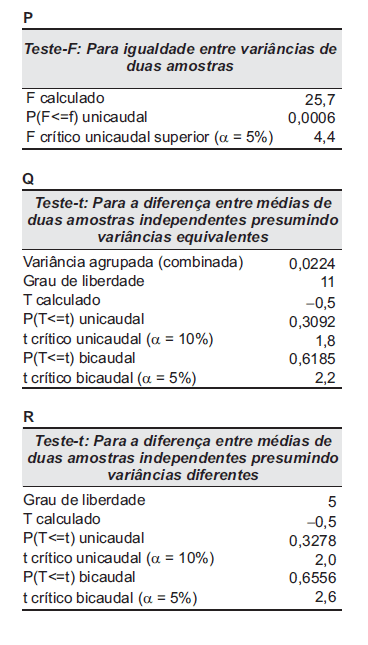
Com os resultados à esquerda e considerando o nível de significância de 10%, conclui-se que a hipótese de igualdade das variâncias

• A.

  não é rejeitada segundo o teste P e, consequentemente, o teste utilizado para testar a hipótese da viscosidade média da formulação 1 ser igual à de formulação 2 é o teste R, que não rejeita a hipótese nula.

• B.

  não é rejeitada segundo o teste P e, consequentemente, o teste utilizado para testar a hipótese da viscosidade média da formulação 1 ser igual à da formulação 2 é o teste Q, que rejeita a hipótese nula.

• C.

  é rejeitada segundo o teste P e, consequentemente, o teste utilizado para testar a hipótese da viscosidade média da formulação 1 ser igual à da formulação 2 é o teste R, que rejeita a hipótese nula.

• D.

  é rejeitada segundo o teste P e, consequentemente, o teste utilizado para testar a hipótese da viscosidade média da formulação 1 ser igual à da formulação 2 é o teste Q, que não rejeita a hipótese nula.

• E.

  é rejeitada segundo o teste P e, consequentemente, o teste utilizado para testar a hipótese da viscosidade média da formulação 1 ser igual à da formulação 2 é o teste R, que não rejeita a hipótese nula.

Sabendo que o número de veículos que chegam, a cada minuto, a determinado local de uma avenida segue um processo de Poisson homogêneo, julgue os itens a seguir.

Considere que uma contagem de tempo seja iniciada no instante em que um veículo A passe nesse local, e que a partir desse, a contagem se encerre no momento da passagem do décimo veículo. Nessa situação, a distribuição desse tempo entre o primeiro e o décimo veículo segue uma distribuição gama.

• C. Certo
• E. Errado