Questões de Estatística

Com base nessa situação hipotética, supondo, ainda, que a população de clientes tenha sido muito grande; que a amostragem tenha sido aleatória simples; que 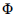(2,0) = 0,977, em que (z) representou a função de distribuição acumulada da distribuição Normal padrão; e que a distribuição t de Student apresenta cauda mais pesada que a distribuição Normal padrão, julgue os itens a seguir.rão, julgue os itens a seguir.

Com nível de confiança de pelo menos 99,6%, a estimativa intervalar para a quantidade média diária de carga movimentada via distribuição t de Student foi 30 ± 7,5 toneladas/dia.

• C. Certo
• E. Errado

Dados os relativos de preços do ano 1 em relação ao ano 0 de quatro produtos e os pesos relativos dos valores de cada produto no ano 0, obtenha o valor mais próximo da variação percentual do Índice de Preços de Laspeyres do ano 1 em relação ao ano 0.

• A.

  9,9%

• B.

  11,3%

• C.

  10,8%

• D.

  10,4%

• E.

  12,0%

Uma pesquisa foi realizada para avaliar o tempo de vida útil, V, de determinado modelo de telefone celular. Sabe-se que a distribuição V segue uma distribuição log normal; isto é, a variável aleatória V é tal que X = 1n(V) segue uma distribuição normal, com média 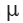 e desvio-padrão  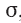, ambos desconhecidos. Uma amostra aleatória simples V₁, V₂, ... Vn foi retirada dessa distribuição de tempos. Com base nessas informações, julgue os itens que se seguem.

A média amostral dos tempos V₁, V₂, ... Vn é uma estimativa de mínimos quadrados para o tempo médio da distribuição V.

• C. Certo
• E. Errado

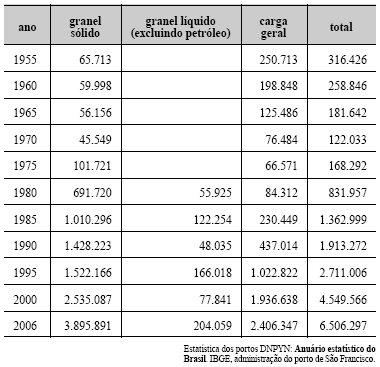
Considerando a tabela acima, que apresenta a movimentação anual de cargas no porto de São Francisco do Sul, em toneladas/ano, julgue os itens de 99 a 103.

A mediana entre todas as quantidades de carga geral mostradas na tabela acima é igual a 84.312.

• C. Certo
• E. Errado

Numa pesquisa realizada em 160 domicílios de uma cidade obteve-se o seguinte gráfico em que o eixo y representa a quantidade de domicílios e o eixo horizontal representa o número de eleitores verificado por domicílio.

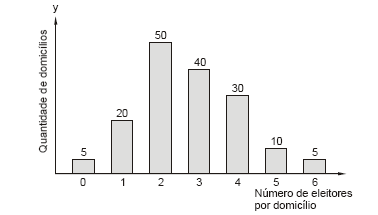
Com relação à média aritmética (Me), número de eleitores por domicílio, a mediana (Md) e a moda (Mo) correspondentes tem-se que:

• A.

  Me = Md e Md < Mo

• B.

  Me < Md < Mo

• C.

  Me < Md e Md > Mo

• D.

  Me < Md e Md = Mo

• E.

  Me > Md e Md = Mo

Efetuando-se o teste qui-quadrado de aderência à distribuição de Bernoulli, a hipótese nula não é rejeitada se o nível de significância for igual a 0,5%.

• C. Certo
• E. Errado

Com base nessa situação hipotética, supondo, ainda, que a população de clientes tenha sido muito grande; que a amostragem tenha sido aleatória simples; que 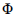(2,0) = 0,977, em que (z) representou a função de distribuição acumulada da distribuição Normal padrão; e que a distribuição t de Student apresenta cauda mais pesada que a distribuição Normal padrão, julgue os itens a seguir.rão, julgue os itens a seguir.

O erro padrão da média amostral foi inferior a 4 toneladas/dia.

• C. Certo
• E. Errado

Uma pesquisa foi realizada para avaliar o tempo de vida útil, V, de determinado modelo de telefone celular. Sabe-se que a distribuição V segue uma distribuição log normal; isto é, a variável aleatória V é tal que X = 1n(V) segue uma distribuição normal, com média 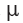 e desvio-padrão  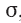, ambos desconhecidos. Uma amostra aleatória simples V₁, V₂, ... Vn foi retirada dessa distribuição de tempos. Com base nessas informações, julgue os itens que se seguem.

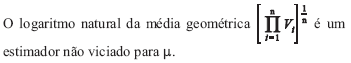
• C. Certo
• E. Errado

Um porto possui dois cais para embarque ou desembarque de passageiros. Cada cais atende a uma única embarcação por vez, e assim que a operação de embarque ou desembarque é concluída, a embarcação deixa imediatamente o local para que a próxima embarcação possa ser atracada ao cais. O número de embarcações que chegam a esse porto por dia, X, segue um processo de Poisson com taxa de chegada igual a 1 embarcação/dia. Se uma embarcação chega ao porto no instante em que os dois cais estão ocupados, ela entra em uma fila única; não havendo limites para o tamanho da fila. Em cada cais, a taxa de serviço é igual a 1,5 embarcação/dia.

Considerando as informações apresentadas acima e que se trata, nessa situação, de um modelo de fila M/M/2 baseado no processo de vida e morte com taxas de chegada e de serviço constantes, julgue os itens subsequentes.

A mediana da distribuição do tempo gasto na operação de embarque ou desembarque é inferior a 1,5 dia/embarcação.

• C. Certo
• E. Errado

Ao analisar o diagrama de dispersão entre duas variáveis aleatórias X e Y, optou-se por utilizar uma forma de relação tal que Y = a + bX para a previsão de Y em função de X (os valores de a e b foram obtidos pelo método dos mínimos quadrados). Estas duas variáveis apresentam um coeficiente de correlação linear igual a r, tal que r > 0. Então, o

• A.

  valor de b poderá ser inferior a zero.

• B.

  coeficiente de correlação linear entre as variáveis (2X) e (5Y) também é igual a r.

• C.

  valor de b é igual ao inverso do valor do coeficiente de correlação linear.

• D.

  coeficiente de correlação linear entre as variáveis (0,5X) e (0,5Y) é igual a 0,5r.

• E.

  valor de b é igual ao coeficiente de correlação linear, pois r > 0.