Questões de Estatística

Tendo como referência as informações acima, julgue os itens de 76 a 83.

Se a amostra estudada representar adequadamente a população em questão, então a probabilidade de uma paciente ter infarto do miocárdio, considerando que ela não usava contraceptivos orais, está compreendida entre 1% e 5%.

• C. Certo
• E. Errado

A função densidade de probabilidade de uma variável aleatória contínua x é dada por:

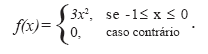
 Para esta função, a média de x, também denominada expectância de x e denotada por E(x) é igual

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

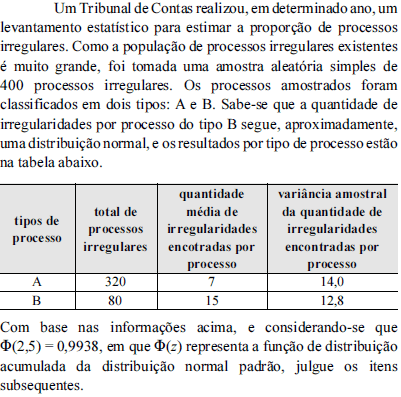
Se um processo do tipo B for selecionado ao acaso, considerando os resultados apresentados na tabela, estima-se que a probabilidade desse processo apresentar 47 ou mais irregularidades é superior a 0,01.

• C. Certo
• E. Errado

Um fabricante faz dois tipos de lâmpadas. Seja X a variável aleatória que representa o tempo de vida do primeiro tipo e Y a variável aleatória que representa o tempo de vida do segundo tipo. Sabe-se que X e Y são independentes e que os respectivos desvios padrões populacionais dos dois tipos são iguais a 250 horas, cada um. Um comprador testou 36 lâmpadas do tipo X e 64 lâmpadas do tipo Y, obtendo 1.000 horas e 1.200 horas de duração média para o tipo X e o tipo Y, respectivamente. Foram formuladas as seguintes hipóteses: H0: μx = μy (hipóteses nula, isto é, a vida média dos tipos X e Y é a mesma) e H1: μx ≠ μy (hipótese alternativa). Considerou-se para o teste que o tamanho das populações é infinito, além de serem normalmente distribuídas e que na distribuição normal padrão (Z) a probabilidade P (Z ≥ zα) = α (0 < α 0,5). Então, pode-se afirmar que a um nível de significância de 2 α

• A.

  H₀ não será rejeitada para zα = 3.

• B.

  H₀ será rejeitada para

• C.

  H₀ será rejeitada para

• D.

  H₀ não será rejeitada, para − 4 < zα < 4.

• E.

  H₀ será rejeitada para qualquer valor de  devido aos valores obtidos pelas amostras.

Uma variável aleatória x tem distribuição densidade de probabilidade dada por: com . Podemos afirmar que o valor de b é igual a:

• A.

  

• B.

  

• C.

  

• D.

  

Com base no texto acima, julgue os itens seguintes.

O coeficiente de explicação é maior que 0,6.

• C. Certo
• E. Errado

Em uma campanha de vacinação, 1.000 empregados de uma grande indústria receberam a vacina contra gripe. Destes, 100 apresentaram alguma reação alérgica de baixa intensidade. A esse respeito, julgue os próximos itens.

Se a distribuição binomial for aproximada por uma distribuição normal e o erro-padrão da média for igual a 0,3, então há uma probabilidade de 95% de que o número médio de empregados da indústria com alguma reação alérgica à vacina esteja entre 99,4 e 100,6.

• C. Certo
• E. Errado

A tabela mostra a distribuição de frequências relativas populacionais (f') de uma variável X:

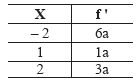
Sabendo que "a" é um número real, então a média e a variância de X são, respectivamente:

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

Os lucros brutos anuais das empresas de um determinado ramo de atividade apresentam uma distribuição normal com média μ e variância populacional σ² desconhecidas. A partir de uma amostra aleatória de tamanho 25 da população considerada de tamanho infinito, deseja-se testar a hipótese H₀: μ = 20 milhões de reais contra a alternativa H₁: μ > 20 milhões de reais, com a realização do teste t de Student. A média e o desvio padrão da amostra são iguais a 23 e 8, respectivamente, em milhões de reais. Seja t_c o valor calculado correspondente para comparar com o valor tabelado t_t da distribuição t de Student, com n graus de liberdade, ao nível de significância α. Então, é correto afirmar que

• A.

  H₀ não será rejeitada, ao nível de significância α, se tt > 1,875 com n = 24.

• B.

  Se H₀ foi rejeitada, ao nível de significância α, tem-se que t_t > 9,375 com n = 24.

• C.

  Se H₀ foi rejeitada, ao nível de significância α, então para um nível de significância superior a α H₀ não seria rejeitada.

• D.

  1,875 < t_c < 9,375 e n = 23.

• E.

  t_c = 9,375 e n = 23.

Considerando que, de acordo com Marshall, os fatores de risco podem ser compreendidos em termos de suas distribuições de probabilidade ao longo de um horizonte de tempo, com modelos muito diferentes sendo úteis conforme a situação seja de curto ou longo prazo, julgue os itens de 101 a 107, acerca de modelos e métodos analíticos.

Quando as distribuições exponencial ou log normal parecem inadequadas e quando as condições de aleatoridade não são satisfeitas, aplica-se a distribuição de Weibull. que serve, entre outras aplicações, para modelar o tempo entre ocorrências, quando a probabilidade de ocorrência muda com o tempo e os índices de falha não são constantes.

• C. Certo
• E. Errado