Questões de Estatística

A moda e a mediana da distribuição da variável aleatória T são, ambas, iguais a horas.

• C. Certo
• E. Errado

O peso de pacotes de café é uma variável aleatória X : N (μ, σ2). Uma máquina de encher pacotes de café está regulada para fazê-lo com μ = 500 g e σ2 = 100 g2. Com o objetivo de manter sob controle a variabilidade do produto, a cada 30 minutos uma amostra aleatória de alguns pacotes é selecionada e testa-se se a variabilidade está controlada. Assim, desejando-se testar H0 : σ2 = 100 contra σ2 ≠ 100 toma-se uma amostra de n = 16 pacotes de café e observa-se para a variância amostral o valor 160 g2. O valor observado da estatística apropriada ao teste é

• A.

  31

• B.

  28

• C.

  24

• D.

  22

• E.

  19

Considere um conjunto de variáveis aleatórias X₁, X₂, ..., X_n X_k X =1, em que cada variável X , k = 1, ..., n, representa o tempo gasto pelo k-ésimo oficial de justiça para o cumprimento de um mandado judicial. Essas variáveis aleatórias são independentes e identicamente distribuídas, segundo uma distribuição normal com média m e desvio padrão d, ambos desconhecidos. A partir dessas informações, julgue os itens de 69 a 76, considerando que 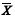 represente a média amostral desse conjunto de variáveis aleatórias.

O desvio médio absoluto, definido por , é uma estatística não-tendenciosa para o desvio padrão d.

• C. Certo
• E. Errado

Com respeito às distribuições Z (normal padrão), t de Student, X² (quiquadrado) e F de Snedecor, julgue os itens que se seguem.

A distribuição t de Student, com k graus de liberdade, é definida pela razão , em que Z é a distribuição normal padrão e Q é a distribuição quiquadrado com k > 0 graus de liberdade, com Z e Q independentes.

• C. Certo
• E. Errado

Tendo como referência as informações acima, julgue os itens de 76 a 83.

O poder para o teste em questão é igual a 0,9, considerando o nível de significância mencionado e o tamanho da amostra igual a 444.

• C. Certo
• E. Errado

Um atributo X tem distribuição normal com média μ e variância populacional igual a 3.600. Uma amostra aleatória de tamanho 100 extraída da população, considerada de tamanho infinito, forneceu uma média de 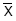 para X. Um teste estatístico é realizado sendo formuladas as hipóteses H0: μ = 200 (hipótese nula) contra H1: μ > 200 (hipótese alternativa). Sabe-se que H0 foi rejeitada a um nível de significância de 5%. Utilizando a informação da distribuição normal padrão (Z) em que a probabilidade  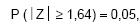tem-se que o valor encontrado para  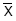foi, no mínimo,

• A.

  219,68

• B.

  214,76

• C.

  209,84

• D.

  204,92

• E.

  200,00

Uma variável aleatória X segue a Distribuição Binomial com média igual a oito e desvio padrão igual a dois. Assim, podemos afirmar que o produto da probabilidade de sucesso p pela probabilidade de insucesso q é igual a:

• A.

  21%

• B.

  25%

• C.

  16%

• D.

  24%

A média, de uma variável aleatória “X”, é considerada uma das medidas de tendência central dos valores numa distribuição estatística.Uma outra medida que tem a maior probabilidade de ocorrência, é denominada de:

• A.

  achatamento;

• B.

  assimetria;

• C.

  mediana

• D.

  percentil;

• E.

  moda

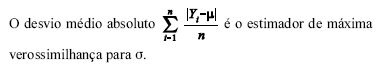
• C. Certo
• E. Errado

Em um estudo oncológico, foi registrado o tempo, em semanas, de sobrevida de pacientes com leucemia aguda. Na data do diagnóstico da patologia, registrou-se também o número de glóbulos brancos, em escala logarítmica. Por meio de uma análise exploratória de dados, assumiu-se que os tempos de sobrevida ti , i = 1, ..., n, em que n é o tamanho da amostra, seguem distribuição exponencial. A tabela a seguir apresenta medidas-resumo, calculadas por meio de um software estatístico, na qual o tempo de sobrevida dos pacientes está em unidade de tempo apropriada, e o número de glóbulos brancos está em logaritmo neperiano (ln).

Se o número de glóbulos brancos seguisse distribuição lognormal, com parâmetros, então o logaritmo do número de glóbulos brancos teria distribuição normal com média e desvio padrão .

• C. Certo
• E. Errado