Questões de Estatística

Um estudo realizado em uma população de tamanho infinito objetiva detectar a proporção de habitantes que possui determinado atributo. Uma amostra piloto adequada forneceu um valor de 25% para essa proporção. Deseja-se um intervalo de confiança de 95% para a estimativa dessa proporção, tendo o intervalo uma amplitude de 5%. Considerando a distribuição amostral da freqüência relativa dos habitantes possuidores do atributo normal e utilizando a informação da distribuição normal padrão (Z) que a probabilidade P(−2 ≤ Z ≤ 2) = 95%, temse que o tamanho da amostra deve ser de

• A.

  1.000

• B.

  1.200

• C.

  1.500

• D.

  1.800

• E.

  2.000

Considere uma amostra aleatória simples X₁, X₂, ..., X_n de uma distribuição com função de distribuição acumulada F(x), em que x é um número real. Para essa amostra, a função de distribuição acumulada empírica é definida como 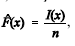 , em que I(x) é o número de elementos na amostra que são iguais ou inferiores a x. Com referência a essa situação, julgue os seguintes itens.

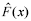é um estimador não-viciado (ou não-tendencioso) para F(x).

• C. Certo
• E. Errado

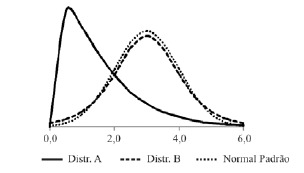
Considerando as densidades de probabilidade ilustradas na figura acima, julgue os itens que se seguem a respeito dos momentos dessas distribuições.

Se a distribuição de B não for normal, então sua curtose é negativa.

• C. Certo
• E. Errado

Considere que, em um ambiente de trabalho industrial, as seguintes medições acerca da poluição do ar tenham sido observadas: 1, 6, 4, 3, 2, 3, 1, 5, 1, 4. Nessas situação, julgue os itens que se seguem.

A variância amostral é superior a 2,8.

• C. Certo
• E. Errado

Das lâmpadas fabricadas por uma companhia extrai-se uma amostra de 100 lâmpadas e obtém-se a vida média de 1.000 horas. A vida das lâmpadas apresenta uma distribuição normal com um desvio padrão populacional igual a 100 horas. Considerando-se a população de tamanho infinito e a informação da distribuição normal padrão (Z), segundo a qual a probabilidade P(Z > 1,64) = 5%, obtémse um intervalo de confiança de 90% para a vida média das lâmpadas. A amplitude deste intervalo é igual a

• A.

  32,8 horas.

• B.

  36,0 horas.

• C.

  40,8 horas.

• D.

  60,0 horas.

• E.

  82,0 horas.

Considere uma amostra aleatória simples X₁, X₂, ..., X_n de uma distribuição com função de distribuição acumulada F(x), em que x é um número real. Para essa amostra, a função de distribuição acumulada empírica é definida como 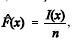 , em que I(x) é o número de elementos na amostra que são iguais ou inferiores a x. Com referência a essa situação, julgue os seguintes itens.

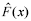é um estimador consistente para F(x).

• C. Certo
• E. Errado

       Um estudo sobre a segmentação do mercado de trabalho comparou o salário daquele que trabalha por conta própria (Y, em R$ mil) com o salário daquele que tem a carteira assinada (X, em R$ mil). Foi ajustado um modelo de regressão linear na forma Y = ax + b + g, em que a e b são os coeficientes do modelo e g representa um erro aleatório com média zero e desvio-padrão 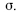 As estimativas de mínimos quadrados ordinários para os coeficientes a e b foram respectivamente iguais a 0,5 e R$ 6 mil. A quantidade de observações utilizadas para o ajuste do modelo foi igual a 400, e os desvios-padrão amostrais de Y e X foram, respectivamente, iguais a R$ 2 mil e R$ 1,5 mil.

Com base nessas informações, julgue os itens subseqüentes.

A estimativa da variância de â, em que â é o estimador de mínimos quadrados para a, é superior a 0,01.

• C. Certo
• E. Errado

Sejam duas populações normalmente distribuídas de tamanho infinito e com a mesma variância σ² desconhecida. Deseja-se testar, ao nível de significância de 5%, que não há diferença entre as médias das duas populações. Para isso, utilizou-se uma amostra aleatória de 15 elementos da primeira população e de 12 da segunda, obtendo a seguir as respectivas médias amostrais. Em um teste t de Student, é correto afirmar:

• A.

  Há 5% de probabilidade do teste indicar uma diferença quando realmente ela não existe.

• B.

  O número de graus de liberdade, no caso, é igual a 26.

• C.

  O cálculo que leva à conclusão de rejeitar a hipótese nula, isto é, que as médias são iguais, independe do tamanho de cada amostra.

• D.

  Há 95% de probabilidade do teste mostrar que o procedimento é inadequado para testar a rejeição da hipótese nula.

• E.

  Há 95% de probabilidade do teste revelar que qualquer conclusão é incorreta.

Considere uma amostra aleatória simples X₁, X₂, ..., X_n de uma distribuição com função de distribuição acumulada F(x), em que x é um número real. Para essa amostra, a função de distribuição acumulada empírica é definida como 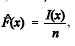 , em que I(x) é o número de elementos na amostra que são iguais ou inferiores a x. Com referência a essa situação, julgue os seguintes itens.

Para cada valor real x, a distribuição amostral de é 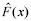assintoticamente normal.

• C. Certo
• E. Errado

A partir dessas informações, julgue os itens seguintes.

A variância da soma X_¹ + X^₂ + X^₃ é igual a 86.

• C. Certo
• E. Errado