Questões de Estatística

Considerando as informações acima, julgue os próximos itens.

A variância da série temporal {X_t} é igual a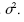

• C. Certo
• E. Errado

Considerando uma variável aleatória X, uniformemente distribuída no intervalo [0, 12], julgue os itens a seguir.

A amplitude de X é igual ao dobro da média de X.

• C. Certo
• E. Errado

Considere as asserções a seguir.

A mediana é uma medida de dispersão de um conjunto de dados.

PORQUE

A mediana é o valor que ocorre com maior freqüência em um conjunto de dados. Analisando-se as asserções, conclui-se que

• A.

  as duas asserções são verdadeiras e a segunda é uma justificativa correta da primeira.

• B.

  as duas asserções são verdadeiras e a segunda não é uma justificativa correta da primeira.

• C.

  a primeira asserção é verdadeira e a segunda é falsa.

• D.

  a primeira asserção é falsa e a segunda é verdadeira.

• E.

  a primeira e a segunda asserções são falsas.

Avalie as afirmativas a seguir acerca de estatísticas suficientes minimais:

I. Uma estatística é suficiente minimal se é suficiente e se é uma função de alguma outra estatística suficiente.

II. Se um estimador de máxima verossimilhança é uma estatística suficiente então ele é uma estatística suficiente minimal.

III. Se um estimador de Bayes é uma estatística suficiente, então ele é uma estatística suficiente minimal.

Assinale:

• A.

  se somente a afirmativa II estiver correta.

• B.

  se somente as afirmativas I e II estiverem corretas.

• C.

  se somente as afirmativas I e III estiverem corretas.

• D.

  se somente as afirmativas II e III estiverem corretas.

• E.

  se todas as afirmativas estiverem corretas.

Com base nessas informações, julgue os itens de 105 a 108.

Considere que o coeficiente de assimetria da distribuição das notas dos alunos tenha sido igual a 1,80. Nessa situação, as proporções de menções A e B observadas foram menores que as proporções esperadas correspondentes.

• C. Certo
• E. Errado

Considerando uma variável aleatória X, uniformemente distribuída no intervalo [0, 12], julgue os itens a seguir.

• C. Certo
• E. Errado

Considere que uma amostra aleatória simples de tamanho n = 5 de uma distribuição Bernoulli com probabilidade de sucesso p seja usada para testar H₀: p = 0,5 versus H₁: p = 0,7 e que seja usado o critério que rejeita a hipótese nula se forem observados 4 ou 5 sucessos. A probabilidade de se cometer erro tipo 1 é igual a:

• A.

  0,1875.

• B.

  0,15625.

• C.

  0,125.

• D.

  0,0625.

• E.

  0,03125.

Considerando as densidades de probabilidade ilustradas na figura acima, julgue os itens que se seguem a respeito dos momentos dessas distribuições.

Se a distribuição B for t de Student, então o seu coeficiente de assimetria será nulo.

• C. Certo
• E. Errado

Uma amostra aleatória simples X1, X2, ..., X16 será retirada de uma população normal com média 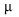e desvio-padrão 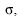, ambos desconhecidos. Para estimá-los, são propostas as estatísticas 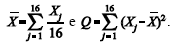. Com base nessas informações, julgue os itens seguintes.

Para a estimação da média populacional 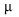, a média amostral é um estimador não tendencioso de mínima variância. Qualquer outro estimador não tendencioso para a estimação de 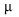, como, por exemplo, a mediana amostral, terá um desvio-padrão uniformemente maior que 0,25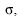

• C. Certo
• E. Errado

Considere que, em um ambiente de trabalho industrial, as seguintes medições acerca da poluição do ar tenham sido observadas: 1, 6, 4, 3, 2, 3, 1, 5, 1, 4. Nessas situação, julgue os itens que se seguem.

A média podada a 20% (ou 20%-trimmed mean) é inferior a 3.

• C. Certo
• E. Errado