Questões de Estatística

Sendo qx a probabilidade de uma pessoa de idade "x" falecer nesta idade "x" e qy a probalidade de uma pessoa de idade "y" falecer nesta idade "y" e px = (1 - qx) e py = (1 - qy), pode-se afi rmar que o resultado da equação [1 - px py] indica:

• a.

  a probabilidade de ambos vivos.

• b.

  a probabilidade de pelo menos um vivo.

• c.

  a probabilidade de pelo menos um morto.

• d.

  a probabilidade de ambos mortos.

• e.

  a probabilidade de "x" vivo e "y" morto ou "y" vivo e "x" vivo.

Julgue os itens a seguir, acerca de noções e conceitos de estatística e de tratamento de dados estatísticos.

• C. Certo
• E. Errado

Em relação às medidas de tendência central, está correto afirmar que:

• A.

  o 1º quartil é sempre superior ao mínimo da amostra.

• B.

  a média nunca é inferior à mediana.

• C.

  a média e a mediana podem coincidir.

• D.

  a moda e a média nunca coincidem.

• E.

  moda e mediana significam a mesma coisa.

As observações de uma variável x são: (0,2,2,1,4,5,5,5,3). Os valores de moda, média e mediana, respectivamente, são:

• A.

  2, 2, 2

• B.

  2, 3, 5

• C.

  3, 3, 5

• D.

  5, 3, 2

• E.

  5, 3, 3

Sorteiam-se ao acaso e sem reposição dois cartões de uma urna contendo cartões numerados de 1 a 5. Sejam as variáveis aleatórias X₁ , o primeiro número sorteado e X ₂ , o segundo número sorteado, pode-se afirmar que as variáveis aleatórias X₁ e X ₂ são:

• A.

  identicamente distribuídas, mas não independentes;

• B.

  independentes, mas não identicamente distribuídas;

• C.

  não correlacionadas e identicamente distribuídas;

• D.

  independentes e identicamente distribuídas;

• E.

  nem independentes, nem identicamente distribuídas.

Seja X uma variável aleatória cuja função geratriz de momentos é dada por

O valor de é:

• A. 1/6
• B. 1/3
• C. 1/2
• D. 2/3
• E. 5/6

Para a resolução das questões que se seguem, lembre-se de que 90% da área abaixo da curva normal padrão se encontram entre -1,645 e 1,645, e 95% da área abaixo da curva normal padrão se encontram entre -1,96 e 1,96.

O tamanho mínimo que deve ter uma amostra aleatória simples para estimar, com 95% de confiança e erro de 1 ponto porcentual, a preferência do eleitorado por determinado candidato é:

• A.

  912.

• B.

  1 200.

• C.

  2 401.

• D.

  4 800.

• E.

  9 604.

Se X₁, X₂,..., X_n representa uma amostra aleatória simples de uma variável aleatória X normalmente distribuída com média µ e desvio padrão desconhecidos, então o estimador de máxima verossimilhança de E[ X² ] é dado por:

• A.
• B.
• C.
• D.
• E.

Considere a tabela a seguir.

A tabela acima apresenta a distribuição de freqüências relativas do valor do salário pago aos funcionários da fábrica Y no mês de abril de 2006. A média e a mediana do valor do salário pago pela fábrica Y no mês de abril de 2006 são, respectivamente,

• A. R$ 200,00 e R$ 400,00
• B. R$ 900,00 e R$ 1000,00
• C. R$ 1050,00 e R$ 1000,00
• D. R$ 800,00 e R$ 800,00
• E. R$ 900,00 e R$ 900,00

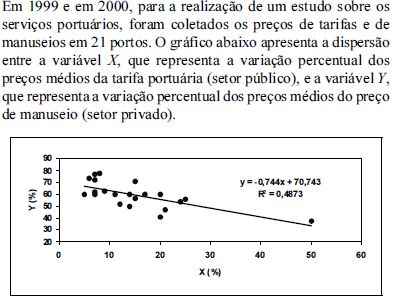
Com relação a esse estudo, julgue os itens a seguir.

A variância amostral de Y é maior do que a variância amostral de X.

• C. Certo
• E. Errado