Questões de Estatística do ano 2007

Sabe-se que existem inúmeros fornecedores de um material X. Porém, somente 60% deles estão aptos a participar de uma licitação para fornecimento do material X para o setor público. Então, a probabilidade de que, numa amostra aleatória simples de 3 destes fornecedores, pelo menos um esteja apto a participar de uma licitação para fornecimento do material X para o setor público é

• A.

  60,0%

• B.

  78,4%

• C.

  80,4%

• D.

  90,4%

• E.

  93,6%

Cada um dos itens subseqüentes contém uma situação hipotética seguida de uma assertiva a ser julgada.

Uma empresa fornecedora de armas possui 6 modelos adequados para operações policiais e 2 modelos inadequados. Nesse caso, se a pessoa encarregada da compra de armas para uma unidade da polícia ignorar essa adequação e solicitar ao acaso a compra de uma das armas, então a probabilidade de ser adquirida uma arma inadequada é inferior a 1/2 .

• C. Certo
• E. Errado

Considerando essas informações, julgue os itens seguintes.

• C. Certo
• E. Errado

A quantidade X de chumbo tetraetílico, em mL por galão, adicionada a certo combustível é uma variável aleatória cuja função de densidade de probabilidade é dada a seguir.

Considerando essas informações, julgue os próximos itens.

A probabilidade de se observar o evento X = 0 é igual a 0,5.

• C. Certo
• E. Errado

Para responder às questões de números 51 e 52, considere o enunciado a seguir.

                    Seja (X,Y) uma amostra aleatória simples, com reposição, de uma distribuição normal com média μ e variância 1. Considere os estimadores L, M, e N de μ dados a seguir:

                    L = 2/3X + 1/3Y; M = 1/4X + 3/4Y; N = 1/2X + 1/2Y.

O erro quadrático médio do estimador M é

• A. 4/9
• B. 5/9
• C. 9/16
• D. 5/8
• E. 4/5

Considere as seguintes afirmações relativas ao modelo de regressão linear com heterocedasticidade.

I. Os estimadores de mínimos quadrados usuais são viciados e não têm variância mínima.

II. Uma forma de se detectar a existência de heterocedasticidade é através da análise de resíduos.

III. As estimativas das variâncias dos parâmetros estimados pelo método de mínimos quadrados usuais serão viciadas.

IV. Uma forma de se detectar a existência de heterocedasticidade é através do método de Newton-Raphson.

Está correto o que se afirma APENAS em

• A. II e III.
• B. I, II e III.
• C. I, II e IV.
• D. I e III.
• E. II, III e IV.

O enunciado a seguir refere-se às questões de n^os 67 e 68. Avaliações de terrenos baseiam-se, geralmente, em modelos de regressão linear nos quais o preço de venda é uma função de algumas variáveis tais como o tamanho do terreno, suas condições e localização. Uma amostra de terrenos comercializados no último mês coletou dados sobre o preço da venda, em R$ 1 000,00, o tamanho do terreno, em m2, e a distância ao centro da cidade, em km. Primeiramente obteve-se o modelo com apenas a variável tamanho do terreno, X1, como explicativa do preço de venda. Os principais quantitativos relativos a esse modelo foram calculados como:

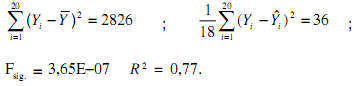
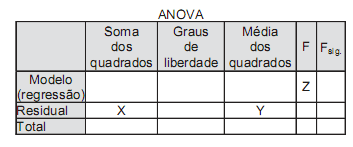
Considerando o quadro acima, os valores de X, Y e Z, respectivamente, são:

• A. 2826, 121 e 3,65E−07
• B. 2178, 121 e 0,77
• C. 2178, 36 e 0,77
• D. 648, 36 e 60,5
• E. 32,4, 18 e 34,1

O enunciado a seguir refere-se às questões de n^os 67 e 68. Avaliações de terrenos baseiam-se, geralmente, em modelos de regressão linear nos quais o preço de venda é uma função de algumas variáveis tais como o tamanho do terreno, suas condições e localização. Uma amostra de terrenos comercializados no último mês coletou dados sobre o preço da venda, em R$ 1 000,00, o tamanho do terreno, em m2, e a distância ao centro da cidade, em km. Primeiramente obteve-se o modelo com apenas a variável tamanho do terreno, X1, como explicativa do preço de venda. Os principais quantitativos relativos a esse modelo foram calculados como:

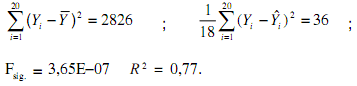
Ao entrar com a variável distância ao centro, o modelo ficou expresso por Yˆ = 9,25 + 2,47 X₁ + 0,78X₂, onde X₁ representa o tamanho do imóvel, em m², e X₂, a distância ao centro, em km. Considerando que todas as variáveis foram testadas e são significativas, analise as afirmações a seguir.

I - Para cada aumento de um metro quadrado no tamanho do terreno, o preço da venda aumenta em 2,47 mil reais, mantendo inalterada a distância ao centro.

II - Para cada aumento de um quilômetro na distância do terreno até o centro, o preço da venda aumenta em 0,78 mil reais, mantendo inalterado o tamanho do terreno.

III - Para um terreno de 40 m², distante do centro 10 km, o preço da venda estimado é de 115,85 mil reais.

É(São) correta(s) a(s) afirmação(ões): (A) I, apenas. (B) II,

• A. I, apenas.
• B. II, apenas.
• C. I e II, apenas.
• D. II e III, apenas.
• E. I, II e III.

Numa análise de regressão simples obteve-se um coeficiente de determinação igual a 0,5625. O coeficiente de correlação linear amostral entre as variáveis em estudo é igual a:

• A.

  0,23;

• B.

  0,56;

• C.

  0,64;

• D.

  0,75;

• E.

  0,80.

Um pesquisador estabeleceu uma relação de proporcionalidade entre duas variáveis de interesse, de modo que a relação 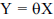 será usada, em que  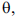o coeficiente de proporcionalidade, é o parâmetro a ser estimado. Observando quatro pares de observações, obteve a seguinte amostra aleatória simples:

• A.

  1,98;

• B.

  2,03;

• C.

  2,12;

• D.

  2,21;

• E.

  2,28.