Questões de Estatística do ano 2008

       Um estudo sobre a segmentação do mercado de trabalho comparou o salário daquele que trabalha por conta própria (Y, em R$ mil) com o salário daquele que tem a carteira assinada (X, em R$ mil). Foi ajustado um modelo de regressão linear na forma Y = ax + b + g, em que a e b são os coeficientes do modelo e g representa um erro aleatório com média zero e desvio-padrão 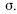 As estimativas de mínimos quadrados ordinários para os coeficientes a e b foram respectivamente iguais a 0,5 e R$ 6 mil. A quantidade de observações utilizadas para o ajuste do modelo foi igual a 400, e os desvios-padrão amostrais de Y e X foram, respectivamente, iguais a R$ 2 mil e R$ 1,5 mil.

Com base nessas informações, julgue os itens subseqüentes.

O valor absoluto da estatística t do teste H₀: a = 0 versus H₀: a 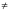0 é superior a 8.

• C. Certo
• E. Errado

A respeito dos testes de hipótese é correto afirmar que

• A.

  quanto maior o p-valor, maior a credibilidade da hipótese alternativa.

• B.

  nível de significância é a probabilidade de se cometer erro do tipo II.

• C.

  o erro do tipo I ocorre quando a hipótese nula não é rejeitada e esta é falsa.

• D.

  o p-valor de um teste é a probabilidade de se cometer erro do tipo I.

• E.

  o poder de um teste é a probabilidade de se rejeitar a hipótese nula quando esta for falsa.

As questões de n^os 53 a 55 referem-se aos diagramas de dispersão a seguir.

O teste de hipótese de que a correlação linear entre Y e X₁ é nula apresentou um valor descritivo (p-value) de 0,480. Conclui-se, então, que

I - a hipótese que 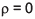 para qualquer nível de significância menor do que 0,480 não deve ser rejeitada;

II - o coeficiente de determinação é menor do que 4,0%;

III - com 48,0% de confiança afirma-se que a relação entre Y e X1 existe, mas é não linear;

IV- a variável Y não deve ser expressa como uma função linear da variável X1.

São corretas APENAS as afirmações

• A.

  I e II

• B.

  III e IV

• C.

  I, II e III

• D.

  I, III e IV

• E.

  II, III e IV

As questões de n^os 57 a 59 referem-se aos resultados de um teste de associação entre as variáveis representadas na tabela de contingência a seguir.

O valor da estatística qui-quadrado e o nível descritivo do teste (p-value) observados foram, respectivamente, X ²=1,811 e 0,770.

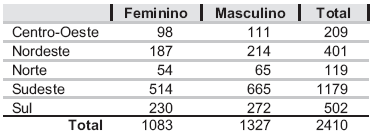
Com relação ao teste de hipótese realizado, considere as afirmações a seguir.

I - O teste foi baseado em 9 graus de liberdade.

II - A hipótese de independência entre Sexo e Região não é rejeitada para qualquer nível de significância inferior a 10,0%.

III - Com 95,0% de confiança afirma-se que existe associação entre as variáveis Sexo e Região.

IV - Sob a hipótese de independência entre as variáveis Sexo e Região, o número esperado de mulheres na região Norte é menor que o número observado.

Estão corretas APENAS as afirmações

• A.

  I e II

• B.

  II e IV

• C.

  II e IV

• D.

  I, III e IV

• E.

  II, III e IV

As questões de n^os 57 a 59 referem-se aos resultados de um teste de associação entre as variáveis representadas na tabela de contingência a seguir.

O valor da estatística qui-quadrado e o nível descritivo do teste (p-value) observados foram, respectivamente, X ²=1,811 e 0,770.

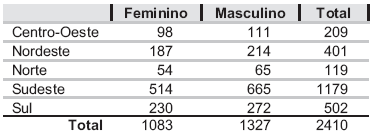
No cálculo da estatística do teste, a menor diferença entre o número de homens observado e o esperado ocorre na região

• A.

  Centro-Oeste

• B.

  Nordeste

• C.

  Sudeste

• D.

  Norte

• E.

  Sul

Com relação aos testes de hipótese sobre um parâmetro de uma população, baseados em uma amostra de tamanho n dessa população, afirma-se que

I - o poder do teste aumenta com 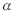 a probabilidade de um erro do tipo I, n mantido constante;

II - o poder do teste não depende de n;

III - o poder do teste é a probabilidade de o teste rejeitar uma hipótese H₀ quando esta é falsa;

IV- o poder do teste é igual a 1 − 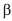 , onde  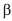é a probabilidade de um erro do tipo II;

Estão corretas APENAS as afirmações

• A.

  I e IV

• B.

  II e III

• C.

  I, II e III

• D.

  I, III e IV

• E.

  II, III e IV

Considere as asserções a seguir.

A região de rejeição de um teste de hipóteses é obtida sob a suposição de que a hipótese da nulidade (H₀) é verdadeira.

PORQUE

Em testes de hipóteses, o erro do tipo I é aquele cometido ao se rejeitar a hipótese da nulidade (H₀) quando esta é verdadeira.

Analisando-se as asserções, conclui-se que

• A.

  as duas asserções são verdadeiras, e a segunda é uma justificativa correta da primeira.

• B.

  as duas asserções são verdadeiras, e a segunda não é uma justificativa correta da primeira.

• C.

  a primeira asserção é verdadeira, e a segunda é falsa.

• D.

  a primeira asserção é falsa, e a segunda é verdadeira.

• E.

  a primeira e a segunda asserções são falsas.

Texto para as questões de 36 a 38

Um pequeno levantamento estatístico foi realizado em dois locais diferentes de atendimento ao público com o objetivo de estimar o número médio de pessoas que diariamente são atendidas nesses locais. Em dez dias de observação, foi registrado o seguinte:

Considere-se a seguinte hipótese nula: os números acima são realizações independentes de uma distribuição de Poisson com média igual a μ, e as observações são pareadas (isto é, em um mesmo dia d foram registrados os números de pessoas atendidas no local X e no local Y).

Ainda com base nas informações apresentadas no texto, assinale a opção correta acerca de testes de hipóteses para comparações entre duas médias.

• A. Embora a distribuição do número de pessoas não seja hipoteticamente normal, o teste t para dados pareados pode ser utilizado para se testar a hipótese apresentada no texto.
• B.

  Considere-se a hipótese alternativa como: "o número médio de pessoas que diariamente são atendidas no local Y é maior do que no local X". Se o teste t para a comparação de médias entre duas populações independentes (observações nãopareadas) for empregado, então a conclusão do teste será a de que a hipótese nula é falsa.

• C.

  Na situação apresentada no texto, o teste da razão de verossimilhança não é apropriado porque, hipoteticamente, a distribuição do número de pessoas não é normal.

• D.

  Sob a hipótese nula, a estimativa do erro padrão da média é inferior a 0,3.

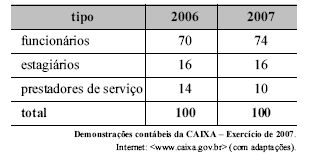
Considerando a tabela acima, que apresenta a distribuição do quadro de colaboradores da CAIXA, em mil pessoas, no final dos anos de 2006 e 2007, julgue os itens seguintes.

Considerando que, para se testar a hipótese nula de que a distribuição do quadro de colaboradores de 2007 manteve-se estatisticamente igual à distribuição de 2006, seja aplicado um teste qui-quadrado, nessa situação, a estatística do teste será igual a 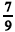 e possuirá 2 graus de liberdade.

• C. Certo
• E. Errado

A probabilidade de significância do teste é inferior a 0,02 e, portanto, hipótese nula é rejeitada caso seja fixado um nível de significância superior a 2%.

• C. Certo
• E. Errado