Questões de Estatística do ano 2008

O poder do teste, que representa a probabilidade de se aceitar corretamente a hipótese nula, é igual a 98,2%.

• C. Certo
• E. Errado

Uma instituição lançará uma campanha nacional entre as indústrias brasileiras com o objetivo de reduzir a probabilidade de ocorrência de acidentes de trabalho. Atualmente, a probabilidade de um operário sofrer algum tipo de acidente é igual a 0,06. Após o lançamento da campanha, espera-se que a probabilidade de um operário sofrer algum tipo de acidente passe a ser inferior a 0,02. Antes de essa empresa lançar a campanha em âmbito nacional, ela realizou um estudo-piloto em um pequeno número de indústrias, adotando o seguinte plano amostral. De um cadastro de indústrias, foram selecionadas aleatoriamente 2 indústrias e nelas aplicaram-se as campanhas propostas pela instituição, envolvendo todos os operários que lá trabalhavam na ocasião do estudo. Essas indústrias são chamadas "caso". Também foram selecionadas aleatoriamente outras 2 indústrias, mas nelas as campanhas não foram aplicadas. Essas são chamadas "controle". Ao longo de um ano foram registrados os números de operários que sofreram algum tipo de acidente nas quatro indústrias, segundo a tabela abaixo.

Com base nas informações apresentadas no texto e na tabela, julgue os itens que se seguem.

Considere-se que a ocorrência de acidentes segue uma distribuição de Poisson e a hipótese nula (H0) do teste é: "a probabilidade de um operário sofrer algum tipo de acidente é igual a 0,06, mas se um operário for exposto à campanha, a probabilidade de ele, operário, sofrer algum tipo de acidente é reduzida para 0,02". A hipótese alternativa (Ha) é: "a probabilidade de um operário sofrer algum tipo de acidente é igual a 0,06, independentemente de o operário ter sido ou não exposto à campanha". Nessa situação, se a estatística qui-quadrado sob H0 for igual a Q0 e se a estatística qui-quadrado sob Ha for igual a Qa, então é correto afirmar que a razão Q0/Qa é a estatística de razão de verossimilhança para o teste em questão.

• C. Certo
• E. Errado

Para que um município possa participar de um projeto na área educacional, a média das notas dos estudantes de 5.ª série a 8.ª série das escolas públicas localizadas nesse município deverá ser igual ou superior a 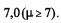  Como não foi possível coletar os dados de todos os estudantes, retirou-se uma amostra aleatória simples de 625 estudantes. Por um teste estatístico, não há evidências estatísticas contra a hipótese de que as notas dos estudantes seguem uma distribuição normal. A nota média observada na amostra foi igual a 6,5 e o desvio padrão amostral foi igual a 2,5. Considerando a situação hipotética apresentada no texto, julgue os itens que se seguem.

O teste de aderência baseada na estatística qui-quadrado é apropriado para avaliar a hipótese de que as notas dos estudantes seguem uma distribuição normal.

• C. Certo
• E. Errado

Com relação ao texto e considerando que a amostra de 100 dias seja aleatória simples, julgue os próximos itens.

Considere as hipóteses nula e alternativa, dadas respectivamente por H₀: m = 25 e H_A: m 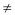25, em que m representa a média populacional. Pelo teste t, há fortes evidências para se rejeitar H₀.

• C. Certo
• E. Errado

O custo mensal de manutenção C de um aparelho é uma variável aleatória normalmente distribuída com variância populacional igual a 900 (R$)². Para testar a hipótese nula H₀ : μ = R$ 175,00 contra a alternativa H1 : μ ≠ R$175,00 será usada uma amostra de 36 aparelhos (μ é a média da população). Fixando-se o nível de significância (α) em 5%, considerando a população de tamanho infinito e sabendo que na distribuição normal padrão (Z) a probabilidade P(Z > 2) = 2,5%, rejeita-se H₀ caso a média da amostra seja

• A.

  inferior a R$ 167,00.

• B.

  superior a R$ 167,00 e inferior a R$ 187,00.

• C.

  igual a R$ 184,00.

• D.

  superior a R$ 115,00 e inferior a R$ 235,00.

• E.

  inferior a R$ 165,00 ou superior a R$ 185,00.

Um grande fabricante de farinha em uma cidade alega que cada pacote produzido pela sua fábrica não contém menos que 1 kg de farinha. Uma amostra de 16 pacotes apresentou uma média de 0,9 kg e desvio padrão de 0,1 kg. Supondo que a quantidade de farinha em cada pacote tenha uma distribuição normal com média μ e variância desconhecida, deseja-se saber se o fabricante tem razão a um determinado nível de significância α. Seja H₀ a hipótese nula do teste (μ = 1 kg), H₁ a hipótese alternativa (μ < 1 kg) e t_α < 0 o quantil da distribuição t de Student, no nível de significância α, para teste unicaudal com 15 graus de liberdade. Sabendo-se que pelo teste t de Student H₀ foi rejeitada, então

• A.

  tem-se que H₀ seria rejeitada para qualquer nível de significância, pois 0,9 < 1.

• B.

  para um nível de significância β, tal que β > α, H₀ não seria rejeitada.

• C.

  o valor da estatística obtido por meio da amostra para comparação com t_α é igual a − 1.

• D.

  o número de graus de liberdade, no caso, não interfere na obtenção de t_α.

• E.

  

Um fabricante divulga que a característica principal de seu produto tem uma média de 1 000 unidades. Um pesquisador, duvidando desta afirmação, encontrou uma característica média de 935 e desvio-padrão amostral de 130 examinando uma amostra aleatória simples de tamanho 9 destes produtos. Calcule o valor mais próximo da estatística t para testar a hipótese nula de que a média da característica principal do produto é 1 000, admitindo que a característica tem uma distribuição normal.

• A.

  -1,5.

• B.

  -1,78.

• C.

  -1,89.

• D.

  -1,96.

• E.

  -2,115.

A análise de variância de um modelo estatístico de regressão linear ordinária com uma variável dependente, um termo constante mais três variáveis como regressores, forneceu uma soma dos quadrados devido à regressão de 13 590 e uma soma dos quadrados dos resíduos de 6 795. Dado que foram usadas 14 observações, calcule o valor mais próximo da estatística F para o teste de hipótese da não-existência da regressão linear estudada.

• A.

  2.

• B.

  5.

• C.

  6,67.

• D.

  7.5.

• E.

  10.

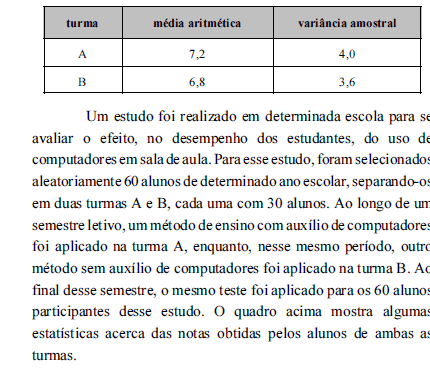
Considerando essas informações, acerca de probabilidade, inferência e amostragem, julgue os itens a seguir.

Sob a hipótese nula de que as distribuições das notas de ambas as turmas são normais e identicamente distribuídas, a estatística do teste t para a comparação dessas duas médias amostrais segue uma distribuição t de Student com 58 graus de liberdade.

• C. Certo
• E. Errado

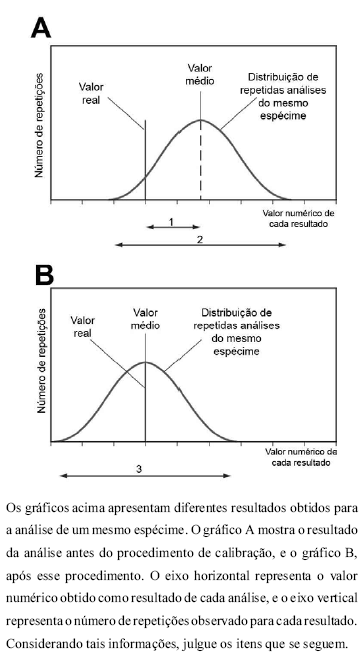
Para que se possa realizar o teste e elaborar os gráficos mostrados é necessário que se conheça previamente o resultado correto esperado para a análise realizada.

• C. Certo
• E. Errado