Questões de Estatística do ano 2008

Suponha que uma livraria possua em seu estoque dois exemplares de uma revista. Considere que Xt seja um processo estocástico de Markov que representa o número de exemplares no estoque no dia t. A matriz de transição de estados é dada por . O elemento Pij da matriz P representa a probabilidade de transição do estado i do dia t para o estado j no dia seguinte t+1; os valores i e j representam os valores do espaço de estados, que podem assumir valores zero, um ou dois.

Com base nas informações apresentadas, julgue os itens que se seguem.

Considerando-se que no dia t a livraria possua em seu estoque dois exemplares da revista, é correto afirmar que, nessa situação, a probabilidade de que no dia t+2 a livraria ainda possua em seu estoque esses dois exemplares é inferior a 0,2.

• C. Certo
• E. Errado

Suponha que uma livraria possua em seu estoque dois exemplares de uma revista. Considere que Xt seja um processo estocástico de Markov que representa o número de exemplares no estoque no dia t. A matriz de transição de estados é dada por . O elemento Pij da matriz P representa a probabilidade de transição do estado i do dia t para o estado j no dia seguinte t+1; os valores i e j representam os valores do espaço de estados, que podem assumir valores zero, um ou dois.

Com base nas informações apresentadas, julgue os itens que se seguem.

No limite estacionário, .

• C. Certo
• E. Errado

Suponha que uma livraria possua em seu estoque dois exemplares de uma revista. Considere que Xt seja um processo estocástico de Markov que representa o número de exemplares no estoque no dia t. A matriz de transição de estados é dada por 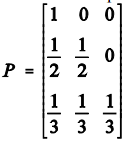. O elemento Pij da matriz P representa a probabilidade de transição do estado i do dia t para o estado j no dia seguinte t+1; os valores i e j representam os valores do espaço de estados, que podem assumir valores zero, um ou dois.

Com base nas informações apresentadas, julgue os itens que se seguem.

Se, nos dias t, t+1 e t+2, a livraria possuir em seu estoque um exemplar da revista, a probabilidade de que essa quantidade seja mantida no dia seguinte t+3 será superior a 0,4.

• C. Certo
• E. Errado

Suponha que uma livraria possua em seu estoque dois exemplares de uma revista. Considere que Xt seja um processo estocástico de Markov que representa o número de exemplares no estoque no dia t. A matriz de transição de estados é dada por 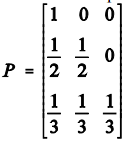. O elemento Pij da matriz P representa a probabilidade de transição do estado i do dia t para o estado j no dia seguinte t+1; os valores i e j representam os valores do espaço de estados, que podem assumir valores zero, um ou dois.

Com base nas informações apresentadas, julgue os itens que se seguem.

Todos os estados do processo estocástico Xt são comunicantes; logo, todos os estados são recorrentes.

• C. Certo
• E. Errado

Suponha que uma livraria possua em seu estoque dois exemplares de uma revista. Considere que Xt seja um processo estocástico de Markov que representa o número de exemplares no estoque no dia t. A matriz de transição de estados é dada por 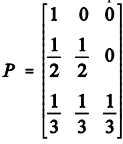. O elemento Pij da matriz P representa a probabilidade de transição do estado i do dia t para o estado j no dia seguinte t+1; os valores i e j representam os valores do espaço de estados, que podem assumir valores zero, um ou dois.

Com base nas informações apresentadas, julgue os itens que se seguem.

Na situação apresentada, a cadeia de Markov é irredutível.

• C. Certo
• E. Errado

Suponha que uma livraria possua em seu estoque dois exemplares de uma revista. Considere que Xt seja um processo estocástico de Markov que representa o número de exemplares no estoque no dia t. A matriz de transição de estados é dada por . O elemento Pij da matriz P representa a probabilidade de transição do estado i do dia t para o estado j no dia seguinte t+1; os valores i e j representam os valores do espaço de estados, que podem assumir valores zero, um ou dois.

Com base nas informações apresentadas, julgue os itens que se seguem.

O processo X é duplamente estocástico.

• C. Certo
• E. Errado

Suponha que uma livraria possua em seu estoque dois exemplares de uma revista. Considere que Xt seja um processo estocástico de Markov que representa o número de exemplares no estoque no dia t. A matriz de transição de estados é dada por 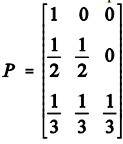. O elemento Pij da matriz P representa a probabilidade de transição do estado i do dia t para o estado j no dia seguinte t+1; os valores i e j representam os valores do espaço de estados, que podem assumir valores zero, um ou dois.

Com base nas informações apresentadas, julgue os itens que se seguem.

Do ponto de vista de séries temporais, Xt segue um processo ARMA(1,0).

• C. Certo
• E. Errado

Suponha que um empresário precise estimar o tempo médio de atendimento em seu restaurante. De uma amostra aleatória de 400 atendimentos, ele observa que a média amostral dos tempos é igual a 1,2 minuto com desvio padrão amostral de 0,8 minuto. A partir de um teste estatístico, esse empresário conclui que a distribuição do tempo de atendimento segue uma distribuição aproximadamente Normal.

 Considerando que Φ(1,96) = 0,975, em que Φ(z) representa a função de distribuição acumulada da distribuição Normal padrão, e com base nas informações apresentadas acima, julgue os itens a seguir.

O erro padrão da média amostral é inferior a 0,1 minuto.

• C. Certo
• E. Errado

Suponha que um empresário precise estimar o tempo médio de atendimento em seu restaurante. De uma amostra aleatória de 400 atendimentos, ele observa que a média amostral dos tempos é igual a 1,2 minuto com desvio padrão amostral de 0,8 minuto. A partir de um teste estatístico, esse empresário conclui que a distribuição do tempo de atendimento segue uma distribuição aproximadamente Normal.

 Considerando que Φ(1,96) = 0,975, em que Φ(z) representa a função de distribuição acumulada da distribuição Normal padrão, e com base nas informações apresentadas acima, julgue os itens a seguir.

A estimativa de máxima verossimilhança do desvio padrão do tempo de atendimento, sob hipótese de normalidade da distribuição dos tempos, é inferior a 0,8 minuto.

• C. Certo
• E. Errado

Suponha que um empresário precise estimar o tempo médio de atendimento em seu restaurante. De uma amostra aleatória de 400 atendimentos, ele observa que a média amostral dos tempos é igual a 1,2 minuto com desvio padrão amostral de 0,8 minuto. A partir de um teste estatístico, esse empresário conclui que a distribuição do tempo de atendimento segue uma distribuição aproximadamente Normal.

 Considerando que Φ(1,96) = 0,975, em que Φ(z) representa a função de distribuição acumulada da distribuição Normal padrão, e com base nas informações apresentadas acima, julgue os itens a seguir.

Com 95% de confiança, a estimativa intervalar para o tempo médio de atendimento é [1,1216 minuto; 1,2784 minuto].

• C. Certo
• E. Errado