Questões de Estatística do ano 2008

Julgue os itens seguintes acerca da distribuição normal.

Se Z representa uma distribuição normal padrão, então X = 5Z + 2 possui distribuição normal com média 2 e variância 5.

• C. Certo
• E. Errado

Para que um município possa participar de um projeto na área educacional, a média das notas dos estudantes de 5.ª série a 8.ª série das escolas públicas localizadas nesse município deverá ser igual ou superior a 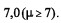  Como não foi possível coletar os dados de todos os estudantes, retirou-se uma amostra aleatória simples de 625 estudantes. Por um teste estatístico, não há evidências estatísticas contra a hipótese de que as notas dos estudantes seguem uma distribuição normal. A nota média observada na amostra foi igual a 6,5 e o desvio padrão amostral foi igual a 2,5. Considerando a situação hipotética apresentada no texto, julgue os itens que se seguem.

O teste de normalidade proposto por Lilliefors é apropriado para avaliar a hipótese de que as notas dos estudantes seguem uma distribuição normal.

• C. Certo
• E. Errado

O elemento X₁ tem distribuição normal padrão.

• C. Certo
• E. Errado

O valor esperado de X X^N é uma matriz simétrica positiva semi-definida.

• C. Certo
• E. Errado

Considere que uma amostra aleatória simples de n indivíduos a ser retirada de uma grande população seja representada por um vetor aleatório X^T = (X₁, X₂ , ..., X_n)^T, em que o índice sobrescrito T indica transposto. A média e o desvio padrão dessa população são iguais a •• e 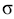, respectivamente. Considere também que U seja um vetor de dimensão n × 1 cujos elementos são todos unitários. Com base nessas informações, julgue os itens a seguir.

Se o vetor aleatório X segue uma distribuição normal multivariada, então a soma X_i + X_j, em que i > j, segue uma distribuição normal com média 2µ.

• C. Certo
• E. Errado

Acerca dos métodos de análise, julgue os itens subseqüentes.

As curvas de distribuição normal mostradas abaixo têm aproximadamente o mesmo desvio-padrão e médias significativamente distintas.

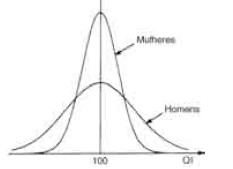
• C. Certo
• E. Errado

Em determinadas circunstâncias, uma variável aleatória binomial pode ser bem aproximada por uma variável aleatória normal. Seja X uma variável aleatória binomial com n=400 e p=1/2. Calcule o valor mais próximo de  usando a aproximação da variável binomial pela normal, dado que    é a função de distribuição de uma variável aleatória normal padrão Z.

• A.

  0,95.

• B.

  0,97.

• C.

  0,98.

• D.

  0,984.

• E.

  0,99.

Sejam n variáveis aleatórias N(0,1) independentes. A soma de seus quadrados tem uma distribuição de:

• A.

  "t" de Student com n-1 graus de liberdade.

• B.

  "t" de Student com n graus de liberdade.

• C.

  Qui quadrado com n graus de liberdade.

• D.

  Qui quadrado com 2n graus de liberdade.

• E.

  F com 1 grau de liberdade no numerador e n graus de liberdade no denominador.

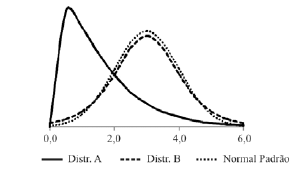
Considerando as densidades de probabilidade ilustradas na figura acima, julgue os itens que se seguem a respeito dos momentos dessas distribuições.

Supondo que a distribuição B seja também normal, então o seu desvio padrão será inferior a 1,0.

• C. Certo
• E. Errado

Com respeito a distribuições conjuntas (X,Y), julgue os itens de 117 a 120.

• C. Certo
• E. Errado